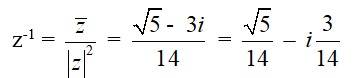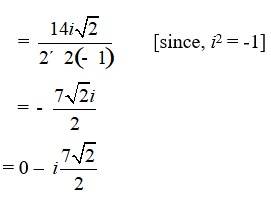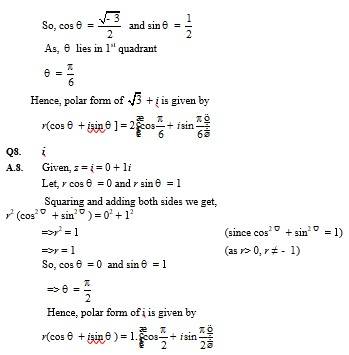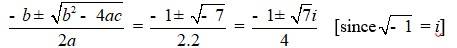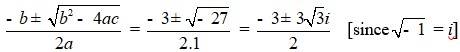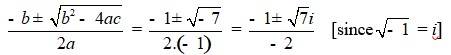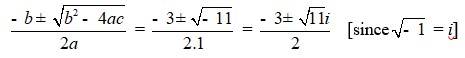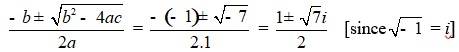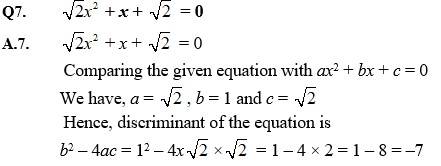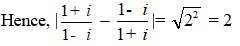NCERT Solutions For Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations: Topics, Questions & Preparation

Exercise 5.1

Express each of the complex number given in the Exercises 1 to 10 in the form a + ib.

 

Q1. (5i)  $\left(\frac{-3}{5}\mathit{}\mathit{i}\right)$

A.1.(5i)  $\left(\frac{-3}{5}i\right)$

= 5  $\left(-\frac{3}{5}\right)$ ×i²          [since i² = –1]

= –3 (–1)

= 3

So, (5i)  $\left(-\frac{3}{5}i\right)$ = 3 + i0

 

Q2. i⁹ + i¹⁹

A.2.  i⁹ + i¹⁹

= i^4x2+1 + i^4x4+3      [Since, i^4k+1 = i and i^4k+3 = – i]

= i – i

= 0

So, i⁹ + i¹⁹ = 0 + i0

 

Q3. i^{– 39}

A.3.  i^{– 39}

=  $\frac{1}{i^{39}}$

=  $\frac{1}{i^{\left(4x9+3\right)}}$

=  $\frac{1}{-i}$ [Since, i^4k+3 = –i]

=  $\frac{1}{-i}$ × $\frac{1}{<br>i}$ $\frac{}{}$ [multiplying numerator and denominator by i]

=  $\frac{i}{-i^2}$

=  $\frac{i}{-\left(-1\right)}$ [since, i² = –1]

= i

So, i ^–39 = 0 + i

 

Q4. 3(7 + i7) + i(7 + i7)

A.4. 3(7 + i7) + i(7 + i7)

= 21 + 21i + 7i + 7i²

= 21 + 28i + 7(–1)[since i² = –1]

= 21 + 28i – 7

= 14 + 28i

 

Q5. (1 – i) – ( –1 + i6)

 A.5. (1 – i) – (–1 + i6)

= 1 – i + 1 – i6

= 2 – 7i

 

Q6. $\left(\frac{1}{5}+i\frac{2}{5}\right)$ –  $\left(4+i\frac{5}{2}\right)$

A.6.  $\left(\frac{1}{5}+i\frac{2}{5}\right)$ –  $\left(4+i\frac{5}{2}\right)$

=  $\frac{1}{5}$ +  $i\frac{2}{5}$ – 4 –  $i\frac{5}{2}$

=  $\frac{1}{5}$ – 4 + i  $\left(\frac{2}{5}-\frac{5}{2}\right)$

=  $\frac{1-20}{5}$ + i  $\left(\frac{4-25}{10}\right)$

=  $\frac{-19}{5}$ + i  $\left(\frac{-21}{10}\right)$

=  $\frac{-19}{5}$ – i  $\frac{21}{10}$

 

Q7. $\left[\left(\frac{1}{3}+i\frac{7}{3}\right)+\left(4+i\frac{1}{3}\right)\right]-\left(-\frac{4}{3}+i\right)$

A.7.  $\left[\left(\frac{1}{3}+i\frac{7}{3}\right)+\left(4+i\frac{1}{3}\right)\right]-\left(-\frac{4}{3}+i\right)$

=  $\frac{1}{3}$ +  $i\frac{7}{3}$ + 4 +  $i\frac{1}{3}$ +  $\frac{4}{3}$ – i

=  $\left(\frac{1}{3}+4+\frac{4}{3}\right)+i\left(\frac{7}{3}+\frac{1}{3}-1\right)$

=  $\frac{1+12+4}{3}$ +  $i\frac{7+1-3}{3}$

=  $\frac{17}{3}$ +  $i\frac{5}{3}$

 

Q8. (1 – i)⁴

A.8. (1 – i)⁴

= [(1 – i)²]²

= [1 + i² – 2.i]²     [since, (a - b)² = a² + b² – 2ab]

= [1 – 1 – 2i]²       [since, i² = – 1]

= (–2i)²

= 4i²

= – 4

= – 4 + 0i

 

Q9. ${\left(\frac{1}{3}+3i\right)}^3$

A.9.  ${\left(\frac{1}{3}+3i\right)}^3$

=  ${\left(\frac{1}{3}\right)}^3+{\left(3i\right)}^3+3\left(\frac{1}{3}\right)\left(3i\right)\left(\frac{1}{3}+3i\right)$ [since, (a + b)³ = a³ + b³ + 3ab(a + b)]

=  $\frac{1}{27}+27i^3+3i\left(\frac{1}{3}+3i\right)$ [since, i³ = i².i = –i and i² = –1]

=  $\frac{1}{27}$ + 27(–i) +  $\frac{3i}{3}$ + (3i× 3i)

=  $\frac{1}{27}$ – 27i + i – 9

=  $\left(\frac{1}{27}-9\right)$ + i(–27 + 1)

=  $\frac{-242}{27}$ – i26

 

Q10. ${\left(-2-\frac{1}{3}i\right)}^3$

A.10. ${\left(-2-\frac{1}{3}i\right)}^3$

=  ${\left[-\left(2+\frac{1}{3i}\right)\right]}^3$

=  ${\left(-1\right)}^3\left[{\left(2+\frac{1}{3}i\right)}^3\right]$

=  $(-8)\left[8+\frac{i^3}{27}+3.2.\frac{1}{3}i\left(2+\frac{i}{3}\right)\right]$ [since, (a + b)³ = a³ + b³ + 3ab(a + b)]

= (–1)  $\left[8-\frac{i}{27}+(2i\times 2)+\left(2i\times \frac{i}{3}\right)\right]$ [since, i³ = i².i = –i and i² = –1]

= (–1)  $\left[8-\frac{i}{27}+4i+\frac{2i^2}{3}\right]$

= (–1)  $\left[8-\frac{2}{3}+i\left(4-\frac{1}{27}\right)\right]$

=  $-\frac{22}{3}$  $–\frac{i107}{27}$

Find the multiplicative inverse of each of the complex numbers given in the Exercises 11 to 13.

 

Q11. 4 – 3i

A.11. Let Z = 4 – 3i

Then  $\bar{z}$ = 4 + 3i

And, z|² = 4²+(-3)²= 16 + 9 = 25

Hence, z^-1 = $\frac{\bar{z}}{{\left|z\right|}^2}$ =  $\frac{4+3i}{25}$ =  $\frac{4}{25}$ +  $i\frac{3}{25}$

 

Q12. √5 $$ + 3i

A.12. Let z = √5 $$ $$ + 3i

Then,  $\bar{z}$ = √5 $$ $$ - 3i

And, |z|² = ( √5 $$ $$ )2 + (3)² = 5 + 9 = 14

So, multiplicative inverse of √5 $$ $$ + 3i is given by

 

Q13. –i

A.13. Let z = -i

Then  $\bar{z}$ = i

And |z|² = (-1)² = 1

So, multiplicative inverse of –i is given by

z^-1 = $\frac{\bar{z}}{\left|z\right|}$ =  $\frac{i}{1}$ = i = 0 + i1

 

Exercise 5.2

Find the modulus and the arguments of each of the complex numbers in Exercises 1 to 2.

 

Exercise 5.3

Q1. x²+ 3 = 0

A.1. x² + 3 = 0

=>x² = –3

=>x =  $\pm \surd 3$

=>x= ± √3 $i$ [since, √-1 $$ = i]

=>x = 0 ± √3 $i$

 

Q2. 2x² + x + 1 = 0

A.2. 2x² + x + 1 = 0

Comparing the given equation with ax² + bx + c = 0, a = 2, b = 1 and c = 1

Hence, discriminant of the equation is

b² – 4ac = 1² – 4 ×2×1 = 1 – 8 = –7

Therefore, the solution of the quadratic equation is $\frac{\mathrm{<br>}}{}$

 

Q3. x² + 3x + 9 = 0

A.3. x² + 3x + 9 = 0

Comparing the given equation with ax² + bx + c = 0

We have, a = 1, b = 3 and c = 9

Hence, discriminant of the equation is

b² – 4ac = 3² – 4 × 1× 9 = 9 – 36 = –27

Therefore, the solution of the quadratic equation is $\frac{}{}$

 

Q4. –x² + x – 2 = 0

A.4.  –x² + x – 2 = 0

Comparing the given equation with ax² + bx + c = 0

We have, a = –1, b = 1 and c = –2

Hence, discriminant of the equation is

b² – 4ac = 1² – 4 ×(-1)×(-2) = 1 – 8 = –7

Therefore, the solution of the quadratic equation is $\frac{}{}$

 

Q5. x² + 3x + 5 = 0

A.5. x² + 3x + 5 = 0

Comparing the given equation with ax² + bx + c = 0

We have, a = 1, b = 3 and c = 5

Hence, discriminant of the equation is

b² – 4ac = 3² – 4 × 1 × 5 = 9 – 20 = –11

Therefore, the solution of the quadratic equation is $\frac{}{}$

 

Q6. x² – x + 2 = 0

A.6. x² – x + 2 = 0

Comparing the given equation with ax² + bx + c = 0

We have, a = 1, b = –1 andc = 2

Hence, discriminant of the equation is

b² – 4ac = (-1)² – 4 × 1 × 2 = 1 – 8 = –7

Therefore, the solution of the quadratic equation is $\frac{}{}$

 

MiscellaneousExercise

Q1. Evaluate:

${\left[i^{18}+{\left(\frac{1}{i}\right)}^{23}\right]}^3$

A.1. ${\left[i^{18}+{\left(\frac{1}{i}\right)}^{23}\right]}^3$

=  ${\left[i^{\mathrm{4\prime }<br>4+2}+\frac{1}{i^{\mathrm{4\prime }<br>6+1}}\right]}^3$

=  ${\left[-1+\frac{1}{i}\right]}^3$ [as i^{4 ×k + 2} = –1 and i^{4 ×k + 1} = i]

=  ${\left[-1+\frac{i}{i^2}\right]}^3$

= [–1 – i]³                        [as i² = –1]

= (-1)³ (1 + i)³

= –1 [1³ + i³ + 3 × 1 ×i(1 + i)]                        [since, (a + b)³ = a³ + b³ + 3ab(a + b)]

= –1 [1 – i³ + 3i(1 + i)]

= –1 [1 – i³ + 3i + 3i²]

= –1 [1 – i + 3i – 3]                           [Since, i² = –1 and i³ = i².i = –i]

= –1 [–2 + 2i]

= 2 – 2i

 

Q2. For any two complex numbers z1 and z2, prove that Re (z1 z2) = Re z1 Re z2 – Imz1 Imz2

A.2. To proof, Re (z1z2) = Re z1 Re z2 – Imz1 Imz2

Let z­­₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ be two complex number.

Then, z₁.z₂ = (x₁ + iy₁)(x₂ + iy₂)

=x₁x₂ + ix₁y₂ + ix₂y₁ + i²y₁y₂

= x₁x₂ + ix₁y₂ + ix₂y₁ – y₁y₂            [since, i² = -1]

= (x₁x₂ – y₁y₂) + i(x₁y₂ + x₂y₁)

As, Re(z₁z₂) = (x₁)(x₂) – (y₁)(y₂)

Now, RHS = Re z₁ Re z₂ – Imz₁Imz₂ = x₁x₂ – y₁y₂

Therefore, Re(z₁z₂) = Rez₁Rez₂ – Imz₁Imz₂

Hence proved.

 

Q3. Reduce $\left(\frac{1}{1-4i}-\frac{2}{1+i}\right) \left(\frac{3-4i}{5+i}\right)$ to the standard form.

A.3. $\left(\frac{1}{1-4i}-\frac{2}{1+i}\right)$  $\left(\frac{3-4i}{5+i}\right)$

=  $\left[\frac{1+i-2\left(1-4i\right)}{\left(1-4i\right)\left(1+i\right)}\right]$  $\left[ \frac{3-4i}{5+i}\right]$

=  $\left(\frac{1+i-2+8i}{1+i-4i-4i^2}\right)$  $\left( \frac{3-4i}{5+i}\right)$

=  $\left(\frac{9i-1}{5-3i}\right)$  $\left( \frac{3-4i}{5+i}\right)$

=  $\frac{\left(9i-1\right)\left(3-4i\right)}{\left(5-3i\right)\left(5+i\right)}$

=  $\frac{27i-36i^2-3+4i}{25+5i-15i-3i^2}$

= .. [since, i² = –1]

=  $\frac{33+31i}{28-10i}$

=  $\frac{33+31i}{28-10i}$ ×  $\frac{28+10i}{28+10i}$ [multiplying denominator and numerator by 28 + 10i]

=  $\frac{\left(3\mathrm{3\prime } <br>28\right)+\left(3\mathrm{3\prime }<br>10i\right)+\left(31\mathrm{i\prime } <br>28\right)+\left(31\mathrm{i\prime }<br>10i\right)}{28^2-{\left(10i\right)}^2}$ [since (a – b)(a + b) = a² – b²]

=  $\frac{924+330i+868i+310i^2}{784-100i^2}$

=  $\frac{924+1198i-310}{784+100}$ [since, i² = –1]

=  $\frac{614+1198i}{884}$

=  $\frac{2\left(307+599i\right)}{884}$

=  $\frac{307+599i}{442}$

=  $\frac{307}{442}$ +  $i\frac{599}{442}$

=  $\frac{a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)}{{\left(c^2+d^2\right)}^2}$

=  $\frac{\left(a^2+b^2\right)\left(c^2+d^2\right)}{{\left(c^2+d^2\right)}^2}$

=  $\frac{a^2+b^2}{c^2+d^2}$

Hence proved.

 

Q5. Convert the following in the polar form:

$\frac{1+7i}{{(2-i)}^2},$ (ii)  $\frac{1+3i}{1-2i}$

A.5. i. Given, z =  $\frac{1+7i}{{(2-i)}^2}$

=  $\frac{1+7i}{2^2+i^2-2.2.i}$

=  $\frac{1+7i}{4+i^2-4i}$

=  $\frac{1+7i}{4-1-4i}$ [since,  $i^2$ = -1]

=  $\frac{1+7i}{3-4i}$

=  $\frac{\left(1+7i\right) \times \left(3+4i\right)}{\left(3-4i\right) \times \left(3+4i\right)}$ [multiply denominator and numerator by (3 + 4i)]

=  $\frac{3+4i+21i+28i^2}{3^2-{\left(4i\right)}^2}$ [since, (a – b)(a + b) = a² – b²]

=  $\frac{3+25i-28}{9+16}$ [since,  $i^2$ = -1]

=  $\frac{-25+ 25i}{25}$

=  $\frac{25\left(-1+i\right)}{25}$

= –1 + i

Let, r cos  $\theta$ = –1 and r sin  $\theta$ = 1

Squaring and adding both sides we get,

r² (cos² $\theta$ +sin² $\theta$ ) = (–1)² + 1²

=>r² = 2 (since cos² $\theta$ + sin² $\theta$ = 1)

=>r = √2 $$ (as r> 0, r ≠  $-\surd 2$ )

Solve each of the equation in Exercises 6 to 9.

 

Q11. If a + ib $=\frac{{\left(x+i\right)}^2}{2x^2+1}$ , prove that a2 + b2 $=\frac{{\left(x^2+1\right)}^2}{{\left(2x^2+1\right)}^2}.$

A.11. Let, z = a + ib

=  $\frac{{\left(x+i\right)}^2}{2x^2+ 1}$

=  $\frac{x^2+ i^2+2xi}{2x^2+ 1}$ [since, (a + b)² = a² + b² + 2ab]

=  $\frac{x^2- 1+2xi}{2x^2+ 1}$ [since, i² = –1]

=  $\frac{x^2- 1}{2x^2+ 1}$ +  $\frac{i2x}{2x^2+ 1}$

So, |z|² = a² + b²

=  $\frac{{\left(x^2- 1\right)}^2}{{\left(2x^2+ 1\right)}^2}$ +  $\frac{{(2x)}^2}{{\left(2x^2+ 1\right)}^2}$

=  $\frac{{\left(x^2\right)}^2+ 1^2- 2.x^2.1+ 4x^2}{{\left(2x^2+ 1 \right)}^2}$ [since, (a + b)² = a² + b² + 2ab]

=  $\frac{x^4+ 1-2x^2+ 4x^2}{{\left(2x^2+ 1\right)}^2}$

=  $\frac{x^4+ 2x^2+ 1}{{\left(2x^2+ 1\right)}^2}$

=  $\frac{{\left(x^2+ 1\right)}^2}{{\left(2x^2+ 1\right)}^2}$ [as, (a + b)² = a² + b² + 2ab]

Hence proved.

 

Q12. Let z1 = 2 – i, z2 = –2 + i. Find

$RE\left(\frac{z_1{z}_2}{z_1}\right)$ (ii)  $IM\left(\frac{1}{z_1{z}_1}\right)$

A.12. Z1 = 2 – i, z2 = –2 + i

Z₁z₂= (2 – i)(–2 + i)

= –4 + 2i + 2i – i²

= –4 + 4i + 1  [since, i² = –1]

= –3 + 4i

$\overline{z_1}$ = 2 + i

i.  $\frac{z_1{z}_2}{\overline{z_1}}$ =  $\frac{- 3+4i}{2+i}$

=  $\frac{-3+4i}{2+i}$ ×  $\frac{2-i}{2-i}$ [multiply denominator and numerator by (2 – i)]

=  $\frac{-6+3i+8i-4i^2}{2^2- i^2}$

=  $\frac{-6+11i+4}{4-\left(-1\right)}$ [since, i² = –1]

=  $\frac{-6+4+11i}{4+1 }$

=  $\frac{-2+11i}{5}$

=  $\frac{-2}{5}$ +  $\frac{11}{5}i$

So, Re(  $\frac{z_1{z}_2}{\overline{z_1}}$ ) =  $\frac{-2}{5}$

ii.  $\frac{1}{z_1\overline{z_1}}$ =  $\frac{1}{\left(2-i\right)\left(2+i\right)}$

=  $\frac{1}{2^2- i^2}$

=  $\frac{1}{4+1}$ [since, i² = –1]

=  $\frac{1}{5}$ + 0i

Therefore, Im  $\left(\frac{1}{z_1\overline{z_1}}\right)$ = 0

 

Q13. Find the modulus and argument of the complex number $\frac{1+2i}{1-3i}.$

A.13. Given, z = $\frac{1+2i}{1-3i}$

=  $\frac{1+2i}{1-3i}$ ×  $\frac{1+3i}{1+3i}$ [multiplying denominator and numerator by (1 + 3i)]

=  $\frac{1+3i+2i+6i^2}{1^2- {(3i)}^2}$

=  $\frac{1+5i+6i^2}{1-9i^2}$

=  $\frac{1-6+5i}{1+9}$ [since, i² = –1]

=  $\frac{-5+5i}{10}$

=  $\frac{5\left(-1+i\right)}{10}$

=  $\frac{-1+i}{2}$

=  $\frac{-1}{2}$ +  $\frac{1}{2}i$

Let, r cos  $\theta$ =  $\frac{-1}{2}$ and r sin  $\theta$ =  $\frac{1}{2}$

Squaring and adding both sides we get,

 

Q14. Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of –6 – 24i.

A.14. Let z = (x – iy)(3 + 5i)

= 3x + 5xi – 3yi – 5yi²

= (3x + 5y) + (5x – 3y)i

Given,  $\bar{z}$ = –6 – 24i

=> (3x + 5y) – (5x – 3y)i = –6 – 24i

Equating real and imaginary part,

3x + 5y = –6 ----------- (1)

5x – 3y = 24 ----------- (2)

Multiplying (1) by 3 and (2) by 5 and adding them, we get

9x + 15y + 25x – 15y = –18 + 120

=> 34x = 102

=>x = 102/34 = 3

Putting x = 3 in (1) we get,

3 × 3 + 5y = –6

=> 9 + 5y = –6

=> 5y = –6 – 9

=> 5y = –15

=>y = –15/5 = –3

Hence, the values of x and y are 3 and –3 respectively.

 

Q15. Find the modulus of $\frac{1+i}{1-i}-\frac{1-i}{1+i}$ .

A.15.  $\frac{1+i}{1-i}$ –  $\frac{1-i}{1+i}$

=  $\frac{{\left(1+i\right)}^2- {\left(1-i\right)}^2}{\left(1-i\right)\left(1+i\right)}$

=  $\frac{1^2+i^2+2.1.i –\left(1^2+i^2- 2.1.i\right)}{1^2- i^2}$ [Since, (a + b)² = a² + b² + 2ab;

(a – b)² = a² + b² – 2ab;

a² – b² = (a + b)(a – b)]

=  $\frac{1-1+2i-1+1+2i}{1+1}$ [Since, i² = –1]

=  $\frac{4i}{2}$

= 2i

 

Q16. If (x + iy)3 = u + iv, then show that $\frac{u}{x}+\frac{v}{y}=4\left(x^2-y^2\right)$ .

A.16. (x + iy)3 = u + iv

=>x³ + (iy)³ + 3.x.iy(x + iy) = u + iv   [since, (a + b)³ = a³ + b³ + 3ab(a + b)]

=>x³ – iy³ + 3x²yi + 3xy²i² = u + iv

=>x³ – iy³ + 3x²yi – 3xy² = u + iv                [since, i² = -1]

=> (x³ – 3xy²) + i(3x²y – y³) = u + iv

Equating real and imaginary part we get,

u = x³ – 3xy² and v = 3x²y – y³

Now,  $\frac{u}{x}$ +  $\frac{v}{y}$

=  $\frac{x^3-3x{y}^2}{x}$ +  $\frac{3x^{2}y- y^3}{y}$

=  $\frac{x\left(x^2- 3y^2\right)}{x}$ +  $\frac{y\left(3x^2- y^2\right)}{y}$

= x² – 3y² + 3x² – y²

= 4x² – 4y²

= 4(x² – y²)

Hence proved.

 

Q20. If ${\left(\frac{1+i}{1-i}\right)}^m=1$ , then find the least positive integral value of m.

A.20. We have,

${\left(\frac{1+i}{1-i}\right)}^m$ = 1

=>  ${\left(\frac{1+i}{1-i} \times \frac{1+}{1+}\right)}^m$ = 1 [multiply denominator and numerator of LHS by (1 + i)]

=>  ${\left(\frac{1+i+i+i^2}{1^2- i^2}\right)}^m$ = 1[since, (a – b)(a + b) = a² – b²]

=>  ${\left(\frac{1+2i-1}{1+1}\right)}^m$ = 1[since, i² = –1]

=>  ${\left(\frac{2i}{2}\right)}^m$ = 1

=>i^m = 1

=>i^m = i^4k              [since, i^4k = 1]

So, m = 4k where k = integer

Therefore, least positive integral value of m is,

m = 4 × 1

m = 4