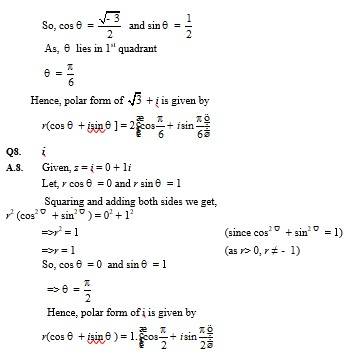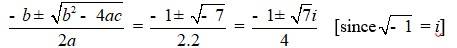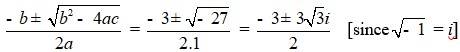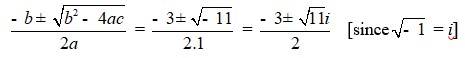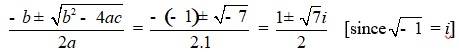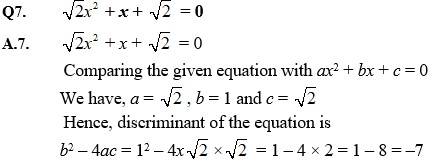Vishal BaghelExecutive Content Operations
NCERT Solutions Maths Class 11 Chapter 5 Complex Numbers and Quadratic Equations are provided on this page. Students can use the Class 11 NCERT Solutions Maths Chapter 5 Complex Numbers and Quadratic Equations to prepare for the board exams. Complex numbers and Quadratic equations is a chapter of high weightage in board exams and entrance exams. Hence students are advised to learn and revise the NCERT Solutions Maths Class 11 Chapter 5 Complex Numbers and Quadratic Equations.
A number of the form a + ib, where a and b are real numbers, is called a complex number. Here a is called the real part, b is called the imaginary part of the complex number and i denotes the square root of -1. Students will learn the algebra of complex numbers in this chapter. Finding the square root of negative real numbers in the set of complex numbers is also explained here.
Complex Numbers and Quadratic Equations - Topics Covered
- Complex Numbers
- Algebra of Complex Numbers
- The Modulus and the Conjugate of a Complex Number
- Argand Plane and Polar Representation
- Quadratic Equation
Check the NCERT Solutions Maths Class 11 Chapter 5 Complex Numbers and Quadratic Equations below.
Q 5.3.1 x2 + 3 = 0
A 5.3.1 x2 + 3 = 0
=>x2 = –3
=>x = ±√3
=>x= ±√3i
[since, √-1 = i]
=>x = 0 ± √3i
Q 5.3.2 2x2 + x + 1 = 0
A 5.3.2 2x2 + x + 1 = 0
- Comparing the given equation with ax2 + bx + c = 0, a = 2, b = 1 and c = 1
- Hence, discriminant of the equation is
- b2 – 4ac = 12 – 4 ×2×1 = 1 – 8 = –7
- Therefore, the solution of the quadratic equation is
- -b ± √(b2-4ac) / 2a = (-1 ± √ 7) / 2.2 = -1 ± √7i / 4
- [since, √-1 = i]
Q 5.3.3 x2 + 3x + 9 = 0
- A 5.3.3
- x2 + 3x + 9 = 0
- Comparing the given equation with ax2 + bx + c = 0
- We have, a = 1, b = 3 and c = 9
- Hence, discriminant of the equation is
- b2 – 4ac = 32 – 4 × 1× 9 = 9 – 36 = –27
- Therefore, the solution of the quadratic equation is
- -b ± √(b2-4ac) / 2a = (-3 ± √ -27) / 2.1 = -3 ± 3√3i / 2
- [since, √-1 = i]
Download Here NCERT Class 11th Maths Chapter 5 Complex Numbers and Quadratic Equations Solutions and PDF
Complex Numbers and Quadratic Equations Solutions and FAQs
Exercise 5.1
Express each of the complex number given in the Exercises 1 to 10 in the form a + ib.
Q1. (5i)
A.1.(5i)
= 5 ×i2 [since i2 = –1]
= –3 (–1)
= 3
So, (5i) = 3 + i0
Q2. i9 + i19
A.2. i9 + i19
= i4x2+1 + i4x4+3 [Since, i4k+1 = i and i4k+3 = – i]
= i – i
= 0
So, i9 + i19 = 0 + i0
Q3. i– 39
A.3. i– 39
=
=
= [Since, i4k+3 = –i]
= × [multiplying numerator and denominator by i]
=
= [since, i2 = –1]
= i
So, i –39 = 0 + i
Q4. 3(7 + i7) + i(7 + i7)
A.4. 3(7 + i7) + i(7 + i7)
= 21 + 21i + 7i + 7i2
= 21 + 28i + 7(–1)[since i2 = –1]
= 21 + 28i – 7
= 14 + 28i
Q5. (1 – i) – ( –1 + i6)
A.5. (1 – i) – (–1 + i6)
= 1 – i + 1 – i6
= 2 – 7i
Q6. –
A.6. –
= + – 4 –
= – 4 + i
= + i
= + i
= – i
Q7.
A.7.
= + + 4 + + – i
=
= +
= +
Q8. (1 – i)4
A.8. (1 – i)4
= [(1 – i)2]2
= [1 + i2 – 2.i]2 [since, (a - b)2 = a2 + b2 – 2ab]
= [1 – 1 – 2i]2 [since, i2 = – 1]
= (–2i)2
= 4i2
= – 4
= – 4 + 0i
Q9.
A.9.
= [since, (a + b)3 = a3 + b3 + 3ab(a + b)]
= [since, i3 = i2.i = –i and i2 = –1]
= + 27(–i) + + (3i× 3i)
= – 27i + i – 9
= + i(–27 + 1)
= – i26
Q10.
A.10.
=
=
= [since, (a + b)3 = a3 + b3 + 3ab(a + b)]
= (–1) [since, i3 = i2.i = –i and i2 = –1]
= (–1)
= (–1)
=
Find the multiplicative inverse of each of the complex numbers given in the Exercises 11 to 13.
Q11. 4 – 3i
A.11. Let Z = 4 – 3i
Then = 4 + 3i
And, z|2 = 42+(-3)2= 16 + 9 = 25
Hence, z-1 = = = +
Q12. √5 + 3i
A.12. Let z = √5 + 3i
Then, = √5 - 3i
And, |z|2 = ( √5 )2 + (3)2 = 5 + 9 = 14
So, multiplicative inverse of √5 + 3i is given by
Q13. –i
A.13. Let z = -i
Then = i
And |z|2 = (-1)2 = 1
So, multiplicative inverse of –i is given by
z-1 = = = i = 0 + i1
Exercise 5.2
Find the modulus and the arguments of each of the complex numbers in Exercises 1 to 2.
Exercise 5.3
Q1. x2+ 3 = 0
A.1. x2 + 3 = 0
=>x2 = –3
=>x =
=>x= ± √3 [since, √-1 = i]
=>x = 0 ± √3
Q2. 2x2 + x + 1 = 0
A.2. 2x2 + x + 1 = 0
Comparing the given equation with ax2 + bx + c = 0, a = 2, b = 1 and c = 1
Hence, discriminant of the equation is
b2 – 4ac = 12 – 4 ×2×1 = 1 – 8 = –7
Therefore, the solution of the quadratic equation is
Q3. x2 + 3x + 9 = 0
A.3. x2 + 3x + 9 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 1, b = 3 and c = 9
Hence, discriminant of the equation is
b2 – 4ac = 32 – 4 × 1× 9 = 9 – 36 = –27
Therefore, the solution of the quadratic equation is
Q4. –x2 + x – 2 = 0
A.4. –x2 + x – 2 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = –1, b = 1 and c = –2
Hence, discriminant of the equation is
b2 – 4ac = 12 – 4 ×(-1)×(-2) = 1 – 8 = –7
Therefore, the solution of the quadratic equation is
Q5. x2 + 3x + 5 = 0
A.5. x2 + 3x + 5 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 1, b = 3 and c = 5
Hence, discriminant of the equation is
b2 – 4ac = 32 – 4 × 1 × 5 = 9 – 20 = –11
Therefore, the solution of the quadratic equation is
Q6. x2 – x + 2 = 0
A.6. x2 – x + 2 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 1, b = –1 andc = 2
Hence, discriminant of the equation is
b2 – 4ac = (-1)2 – 4 × 1 × 2 = 1 – 8 = –7
Therefore, the solution of the quadratic equation is
MiscellaneousExercise
Q1. Evaluate:
A.1.
=
= [as i4 ×k + 2 = –1 and i4 ×k + 1 = i]
=
= [–1 – i]3 [as i2 = –1]
= (-1)3 (1 + i)3
= –1 [13 + i3 + 3 × 1 ×i(1 + i)] [since, (a + b)3 = a3 + b3 + 3ab(a + b)]
= –1 [1 – i3 + 3i(1 + i)]
= –1 [1 – i3 + 3i + 3i2]
= –1 [1 – i + 3i – 3] [Since, i2 = –1 and i3 = i2.i = –i]
= –1 [–2 + 2i]
= 2 – 2i
Q2. For any two complex numbers z1 and z2, prove that Re (z1 z2) = Re z1 Re z2 – Imz1 Imz2
A.2. To proof, Re (z1z2) = Re z1 Re z2 – Imz1 Imz2
Let z1 = x1 + iy1 and z2 = x2 + iy2 be two complex number.
Then, z1.z2 = (x1 + iy1)(x2 + iy2)
=x1x2 + ix1y2 + ix2y1 + i2y1y2
= x1x2 + ix1y2 + ix2y1 – y1y2 [since, i2 = -1]
= (x1x2 – y1y2) + i(x1y2 + x2y1)
As, Re(z1z2) = (x1)(x2) – (y1)(y2)
Now, RHS = Re z1 Re z2 – Imz1Imz2 = x1x2 – y1y2
Therefore, Re(z1z2) = Rez1Rez2 – Imz1Imz2
Hence proved.
Q3. Reduce to the standard form.
A.3.
=
=
=
=
=
= .. [since, i2 = –1]
=
= × [multiplying denominator and numerator by 28 + 10i]
= [since (a – b)(a + b) = a2 – b2]
=
= [since, i2 = –1]
=
=
=
= +
=
=
=
Hence proved.
Q5. Convert the following in the polar form:
(ii)
A.5. i. Given, z =
=
=
= [since, = -1]
=
= [multiply denominator and numerator by (3 + 4i)]
= [since, (a – b)(a + b) = a2 – b2]
= [since, = -1]
=
=
= –1 + i
Let, r cos = –1 and r sin = 1
Squaring and adding both sides we get,
r2 (cos2 +sin2 ) = (–1)2 + 12
=>r2 = 2 (since cos2 + sin2 = 1)
=>r = √2 (as r> 0, r ≠ )
Solve each of the equation in Exercises 6 to 9.
Q11. If a + ib , prove that a2 + b2
A.11. Let, z = a + ib
=
= [since, (a + b)2 = a2 + b2 + 2ab]
= [since, i2 = –1]
= +
So, |z|2 = a2 + b2
= +
= [since, (a + b)2 = a2 + b2 + 2ab]
=
=
= [as, (a + b)2 = a2 + b2 + 2ab]
Hence proved.
Q12. Let z1 = 2 – i, z2 = –2 + i. Find
(ii)
A.12. Z1 = 2 – i, z2 = –2 + i
Z1z2= (2 – i)(–2 + i)
= –4 + 2i + 2i – i2
= –4 + 4i + 1 [since, i2 = –1]
= –3 + 4i
= 2 + i
i. =
= × [multiply denominator and numerator by (2 – i)]
=
= [since, i2 = –1]
=
=
= +
So, Re( ) =
ii. =
=
= [since, i2 = –1]
= + 0i
Therefore, Im = 0
Q13. Find the modulus and argument of the complex number
A.13. Given, z =
= × [multiplying denominator and numerator by (1 + 3i)]
=
=
= [since, i2 = –1]
=
=
=
= +
Let, r cos = and r sin =
Squaring and adding both sides we get,
Q14. Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of –6 – 24i.
A.14. Let z = (x – iy)(3 + 5i)
= 3x + 5xi – 3yi – 5yi2
= (3x + 5y) + (5x – 3y)i
Given, = –6 – 24i
=> (3x + 5y) – (5x – 3y)i = –6 – 24i
Equating real and imaginary part,
3x + 5y = –6 ----------- (1)
5x – 3y = 24 ----------- (2)
Multiplying (1) by 3 and (2) by 5 and adding them, we get
9x + 15y + 25x – 15y = –18 + 120
=> 34x = 102
=>x = 102/34 = 3
Putting x = 3 in (1) we get,
3 × 3 + 5y = –6
=> 9 + 5y = –6
=> 5y = –6 – 9
=> 5y = –15
=>y = –15/5 = –3
Hence, the values of x and y are 3 and –3 respectively.
Q15. Find the modulus of .
A.15. –
=
= [Since, (a + b)2 = a2 + b2 + 2ab;
(a – b)2 = a2 + b2 – 2ab;
a2 – b2 = (a + b)(a – b)]
= [Since, i2 = –1]
=
= 2i
Q16. If (x + iy)3 = u + iv, then show that .
A.16. (x + iy)3 = u + iv
=>x3 + (iy)3 + 3.x.iy(x + iy) = u + iv [since, (a + b)3 = a3 + b3 + 3ab(a + b)]
=>x3 – iy3 + 3x2yi + 3xy2i2 = u + iv
=>x3 – iy3 + 3x2yi – 3xy2 = u + iv [since, i2 = -1]
=> (x3 – 3xy2) + i(3x2y – y3) = u + iv
Equating real and imaginary part we get,
u = x3 – 3xy2 and v = 3x2y – y3
Now, +
= +
= +
= x2 – 3y2 + 3x2 – y2
= 4x2 – 4y2
= 4(x2 – y2)
Hence proved.
Q20. If , then find the least positive integral value of m.
A.20. We have,
= 1
=> = 1 [multiply denominator and numerator of LHS by (1 + i)]
=> = 1[since, (a – b)(a + b) = a2 – b2]
=> = 1[since, i2 = –1]
=> = 1
=>im = 1
=>im = i4k [since, i4k = 1]
So, m = 4k where k = integer
Therefore, least positive integral value of m is,
m = 4 × 1
m = 4
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
News & Updates
Maths Ncert Solutions class 11th Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test