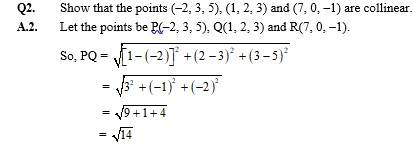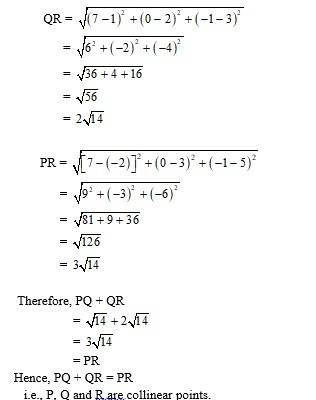Salviya AntonySenior Executive - Content
NCERT Solutions Maths Class 11 Chapter 12 Introduction to Three Dimensional Geometry is given on this page. Students are recommended to learn the Class 11 Maths Solutions Introduction to Three Dimensional Geometry. These solutions are prepared in a detailed manner. Students will find it easy to understand the solutions of NCERT Solutions Maths Class 11 Chapter 12 Introduction to Three Dimensional Geometry given on this page.
Introduction to Three Dimensional Geometry is an important chapter in Maths as far as the board exam is concerned. This is of high weightage for entrance exams too. We have provided the solutions of all the exercises of Chapter 12 Introduction to Three Dimensional Geometry. Topics covered in this chapter are given below. Check Answers to NCERT Solutions Class 11 Maths Chapter 12 – Introduction to Three Dimensional Geometry here.
Topics Covered - Introduction to Three Dimensional Geometry
- Coordinate Axes and Coordinate Planes in Three Dimensional Space
- Coordinates of a Point in Space
- Distance between Two Points
- Section Formula
Students can check the NCERT Solutions Maths Class 11 Chapter 12 Introduction to Three Dimensional Geometry below.
Q 12.3.2 Given that P (3, 2, – 4), Q (5, 4, – 6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR
A 12.3.2 Let point Q divides PR in the k : 1. Then co-ordinate of Q will be
k(9)+1(3) / k+1, K(8)+1(2)/k+1, K(-10)+1(-4)/ K+1
=(5,4,-6) = (9k+3/K+1, 8k+2/K+1, -10k-4/K+1)
Equating the coordinates we get,
9k+3/k+1 = 5
9k+3 = 5(k+1)
9k+3 = 5k+5
9k-5k = 5-3
4k=2
k=2/4
k=1/2
Putting k=1/2 in y-coordinate and z-coordinate
8k+2/k+1
(8x1/2)+2/1/2+1
Download Here NCERT Class 11th Maths Chapter 12 Introduction to Three Dimensional Geometry Solutions PDF
Introduction to Three Dimensional Geometry Solutions and FAQs
Exercise 12.1
Q1. A point is on the x-axis. What are its y-coordinate and z-coordinates?
A.1. When a point lies on x-axis, its y-coordinate and z-coordinate are zero.
Q2. A point is in the XZ-plane. What can you say about its y-coordinate?
A.2. When a point lies on XZ-plane, its y-coordinate is zero.
Q3. Name the octants in which the following points lie:
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (– 4, 2, –5), (– 4, 2, 5), (–3, –1, 6) (– 2, – 4, –7).
A.3.
|
|
|
Octants |
|||||||
|
|
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
| coordinates |
x |
+ |
– |
– |
+ |
+ |
– |
– |
+ |
| y |
+ |
+ |
– |
– |
+ |
+ |
– |
– |
|
| z |
+ |
+ |
+ |
+ |
– |
– |
– |
– |
|
(1, 2, 3) lies in octant I.
(4, –2, 3) lies in octant IV.
(4, –2, –5) lies in octant VIII.
(4, 2, –5) lies in octant V.
(–4, 2, –5) lies in octant VI.
(–4, 2, 5) lies in octant II.
(–3, –1, 6) lies in octant III.
(–2, –4, –7) lies in octant VII.
Q4. Fill in the blanks:
The x-axis and y-axis taken together determine a plane known as_______.
The coordinates of points in the XY-plane are of the form _______.
Coordinate planes divide the space into ______ octants.
A.4. i. The x-axis and y-axis taken together determine a plane known as XY plane.
ii. The coordinates of points in the XY-plane are of the form (x, y, 0).
iii. Coordinate planes divide the space into 8 (eight) octants.
Exercise 12.2
Q1. Find the distance between the following pairs of points:
- (2, 3, 5) and (4, 3, 1)
- (–3, 7, 2) and (2, 4, –1)
- (–1, 3, – 4) and (1, –3, 4)
- (2, –1, 3) and (–2, 1, 3).
A.1. i. The distance between points (2, 3, 5) and (4, 3, 1) is
Exercise 12.3
Q1. Find the coordinates of the point which divides the line segment joining the points (– 2, 3, 5) and (1, – 4, 6) in the ratio (i) 2 : 3 internally, (ii) 2 : 3 externally.
A.1. i.Let P(x, y, z) be the point which divides line segment joining (–2, 3, 5) and (1, –4, 6) internally in the ratio 2 : 3
Therefore,
x = = =
y = = =
z = = =
Thus, the required points are
ii.
Let P(x, y, z) be the point which divides line segment joining (–2, 3, 5) and (1, –4, 6) externally in the ratio 2 : 3
Therefore,
x = = = –8
y = = = 17
z = = = 3
Thus, the required points are (–8, 17, 3).
Q2. Given that P (3, 2, – 4), Q (5, 4, – 6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR.
A.2. Let point Q divides PR in the k : 1. Then co-ordinate of Q will be
=> (5, 4, –6) =
Equating the co-ordinates we get,
= 5
=>
=>
=>
=>
=>
=>
Putting in y-coordinate and z-coordinate
=
= (4 + 2) ÷
= 6 x
= 4
And
= (–5 – 4) ÷
= – 9 x
= – 6
Which is matching with the given co-ordinates of Q.
Hence, the ration in which Q divides PR is k : 1
= : 1
= 1 : 2
Q3. Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8)
A.3. Let YZ-plane divides the line segment joining A(–2, 4, 7) and B (3, –5, 8) at point P (x, y, z) in the ratio k : 1.
Then the co-ordinates of P are.
As P lies on YZ-plane its x-coordinate is zero.
i.e.
=>
=>
Hence the YZ-plane divides AB internally in ratio.
: 1 = 2 : 3
Q4. Using section formula, show that the points A (2, –3, 4), B (–1, 2, 1) and are collinear.
A.4. Let P divides AB in ratio k : 1. Then co-ordinates of point P are
=
Let us examine whether the value of k, the point P coincides with point C
Putting
=>
=>
Put in
=
=
=
And put in
=
=
= 2
Therefore, C is a point which divides AB internally in ratio 2 : 1 and is same as P. Hence A, B and C are collinear.
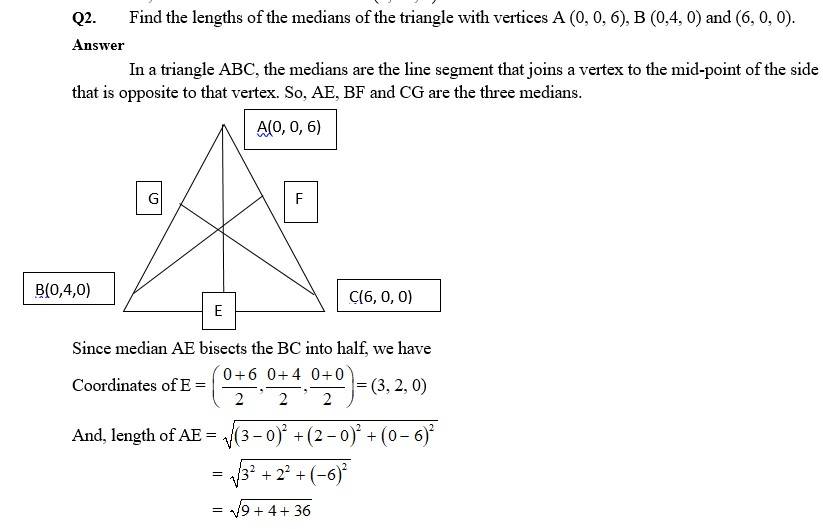
Q5. Find the coordinates of the points which trisect the line segment joining the points P (4, 2, – 6) and Q (10, –16, 6).
A.5. Let A(x1, y1, z1) and B(x2, y2, z2) trisect the line segment joining the points P(4, 2, –6) and Q(10, –16, 6).
Since A divides PQ internally in ratio 1 : 2. Then co-ordinates of A
=
=
=
= (6, –4, –2)
Similarly B divides PQ internally in ratio 2 : 1. Then co-ordinates of B
=
=
=
= (8, –10, 2)
Hence the points which trisects the line segment joining the points P(4, 2, –6) and Q(10, –16, 6) are (6, –4, –2) and (8, –10, 2).
Miscellaneous Example
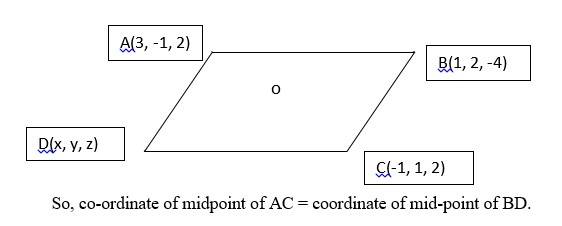
Q1. Three vertices of a parallelogram ABCD are A(3, – 1, 2), B (1, 2, – 4) and C (– 1, 1, 2). Find the coordinates of the fourth vertex.
A.1. Let D(x, y, z) be the fourth vertex of the parallelogram ABCD.
In a parallelogram, the diagonal AC and BD bisects each other at point say O.
=>
=> (1, 0, 2) =
Equating the coordinates we get,
= 1
=>
=>
And
= 0
=>
And
= 2
=>
=>
=>
So, coordinates of fourth vertex is (1, –2, 8)
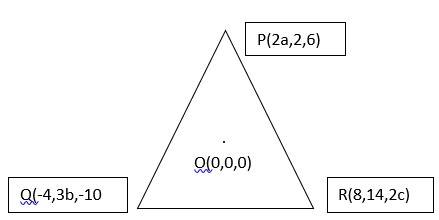
Q3. If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (– 4, 3b, –10) and R(8, 14, 2c), then find the values of a, b and c.
A.3. We know that, the centroid of a triangle with vertices (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) is
So, = (0, 0, 0)
Equating the coordinates we get,
= 0
=>
=>
=>
=>
=>
And,
=>
=>
=>
=>
And,
=>
=>
=>
=>
=>
=>
=>
So the coordinates Q are (0, 2, 0) and (0, –6, 0).
Q5. A point R with x-coordinate 4 lies on the line segment joining the points P(2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.
[Hint Suppose R divides PQ in the ratio k : 1. The coordinates of the point R are given by
A.5. Given, x-coordinate of R = 4
Let R divides line segment joining points P(2, –3, 4) and Q(8, 0,10) internally in the ratio k : 1. Then coordinate of R is
=
Then,
= 4
=>
=>
=>
=>
=>
=>
Hence,
=
=
=
=
And,
z =
=
=
=
= 6
Therefore, coordinates of R is (4, –2, 6).
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
News & Updates
Maths Ncert Solutions class 11th Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test