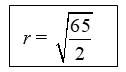NCERT Solutions Maths Class 11 Chapter 11 Conic Sections: Overview, Questions, Preparation

Exercise – 11.1

In each of the following Exercises 1 to 5, find the equation of the circle with

Q1. centre (0,2) and radius 2

A.1. Centre (0, 2) and radius 2 .

Here, h = 0, k = 2, r = 2

Equation of the circle is given by'

(x – h)² + (y – k)² = r²

x² + (y – 2)² = 4

$\Rightarrow x^2+y^2-4y=0$

 

Q2.centre (–2,3) and radius 4

A.2. Centre (–2, 3) and radius 4.

Given, h = –2, k = 3, r = 4

⸫ Equation of the circle is,

(x – h)² + (y – k)² = 2²

(x + 2)² + (y – 3)² = 16

$\Rightarrow x^2+y^2+4x-6y-3=0$

 

Q3.Centre  $\left(\frac{1}{2},\frac{1}{4}\right)$ and radius  $\left(\frac{1}{12}\right)$

A.3. Given,

h =  $\frac{1}{2}$ , k =  $\frac{1}{4}$ , r =  $\frac{1}{12}$

⸫ Equation of the circle is,

(x – h)² + (y – k)² = r²

${\left(x-\frac{1}{2}\right)}^2+{\left\{y-\left(\frac{1}{4}\right)\right\}}^2={\left(\frac{1}{12}\right)}^2$

${\left(x-\frac{1}{2}\right)}^2+{\left(y-\frac{1}{4}\right)}^2=\frac{1}{144}$

 

 

Q9. 2x² + 2y² – x = 0

A.9. 2x² + 2y²= x

2(x² + y²) = x

x² + y² = $\frac{x}{2}$

x² – $\frac{x}{2}$ + y²= 0

x² – 2 $\left(\frac{x}{4}\right)$ + y² = 0

x² – $2\left(\frac{x}{4}\right)+{\left(\frac{1}{4}\right)}^2-{\left(\frac{1}{4}\right)}^2+y^2=0$

x² – $2\left(\frac{1}{4}x\right)+{\left(\frac{1}{4}\right)}^2+y^2={\left(\frac{1}{4}\right)}^2$

Using,

(a – b)² = a² + b² – 2ab,

We get

${\left(x-\frac{1}{4}\right)}^2+{(y-0)}^2={\left(\frac{1}{4}\right)}^2$

Comparing with the equation of a circle (x – h)² + (y – k)² = r²

We get,

h =  $\frac{1}{4}$ , k = 0, r =  $\frac{1}{4}$

⸫Centre = (h, k) =  $\left(\frac{1}{4},0\right)$

Radian = r =  $\frac{1}{4}$

 

Q10. Find the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line 4x + y = 16.

A.10. Let the equation of the circle be,

(x – h)² + (y – k)² = r² -------(i)

Since the circle passes through (4, 1) and (6, 5)

Putting x = 4 and y = 1 in (i),

(4 – h)² + (1 – k)² = 2² ---------(ii)

Putting x = 6 and y = 5 in (i),

(6 – h)² + (5 – k)² = r²---------(iii)

Equating equation (ii) and (iii), We get.

(4 – h)² + (1 – k)² = (6 – h)² + (5 – k)²

4² + h² – 2.4.h + 1² + k² – 2.1.k = 6² + h² – 2.6.h + 5² + k² – 2.5.k

16 + h² – 8h + 1 + k² – 2k = 36 + h² – 12h + 25 + k² – 10k

17 + h² – 8h + k² – 2k = 61 + h²  – 12h + k² – 10k

–8h + 12h – 2k + 10k = 61 – 17

4h + 8k = 44

4(h + 2k) = 44

h + 2k =  $\frac{44}{4}$ = 11-------------(iv)

Since the centre of the circle passes through 4x + y = 16

⸫4h + k = 16

(4h + k = 16) × 2

8h + 2k = 32--------------(v)

Subtract (v) – (iv).

8h + 2k = 32

–(h + 2k = 11)

7h = 21

h =  $\frac{21}{7}$ = 3

Putting h = 3 in (iv), we get

3 + 2k = 11

2k = 11 – 3

k =  $\frac{8}{2}$ = 4

Putting the values of h and k in, (ii)

(4 – 3)² + (1 – 4)² = r²

1² + (–3)² = r²

1 + 9 = r²

r = √10 $$

Thus the equation of the circle is,

(x – 3)² + (y – 4)² = ${(\surd 10)}^2$

(x – 3)² + (y – 4)² = 10

x² ${}_{\mathrm{<br>}}+y^2-6x-8y+15=0$

 

Q11. Find the equation of the circle passing through the points (2,3) and (–1,1) and whose centre is on the line x – 3y – 11 = 0.

A.11. Let the equation of the circle be.

(x – h)² + (y – k)² = r² -----(i)

Since the circle passes through (2, 3) and (–1, 1),

Putting x = 2 and y = 3 in (i),

(2 – h)² + (3 – k)² = r²---------(ii)

Putting x = –1 and y = 1 in (i),

(–1 – h)² + (1 – k)² = r²

Equating equation (ii) and (iii), We get:–

(2 – h)² + (3 – k)² = (–1 – h)² + (1 – k)²

2² + h² – 2.2.h + 3² + k² – 2.3.k = (–1)² + h² – 2.(–1).h + 1² + k² – 2(1)(k)

4 + h² – 4h + 9 + k² – 6k = 1 + h² + 2h + 1 + k² – 2k

13 – 4h – 6k = 2 + 2h – 2k

–4h – 2h – 6k + 2k = 2 – 13

–6h – 4k = 11

–(6h + 4k) = 11

6h + 4k = 11-------(iv)

Since the centre of the circle is on the line x – 3y – 11 = 0

⸫ h – 3k = 11

(h – 3k = 11) × 6 = 6h – 18k = 66-----(v)

Subtract (v) – (iv),

$\begin{array}{l}\cancel{6h}-18k=66\\ \underset{\_}{\left(\cancel{6h}\pm 4k=-11\right)}\end{array}$

– 22k = 55

k =  $\frac{-55}{22}=\frac{-5}{22}$

Putting the value of k in (iv), we get

6h +  $\cancel{\stackrel{\mathrm{2/4}}{}}$ ×  $\left(-\frac{55}{\underset{11}{\cancel{22}}}\right)=11$

6h +  $\left(-\frac{110}{11}\right)=11$

6h = 11 +  $\frac{\cancel{\stackrel{10}{110}}}{\underset{1}{\cancel{11}}}$

6h = 11 + 10

h =  $\frac{{\cancel{21}}^7}{\cancel{\underset{2}{6}}}=\frac{7}{2}$

Putting values of h and k in (ii), we get

${\left(2-\frac{7}{2}\right)}^2+{\left(3+\frac{5}{2}\right)}^2=r^2$

${\left(\frac{4-7}{2}\right)}^2+{\left(\frac{6+5}{2}\right)}^2=r^2$

${\left(\frac{-3}{2}\right)}^2+{\left(\frac{11}{2}\right)}^2=r^2$

$\frac{9}{4}+\frac{121}{4}=r^2$

$\frac{9+121}{4}=r^2$

r² = $\frac{\stackrel{65}{\cancel{130}}}{\cancel{\underset{2}{4}}}$

r² = $\frac{65}{2}$

r =

Than the equation of the circle is,

${\left(x-\frac{7}{2}\right)}^2+{\left(y+\frac{5}{2}\right)}^2=\frac{65}{2}.$

$\Rightarrow x{}_2+y^2-7x+5y-14=0$

 

Q12. Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2,3).

A.12. Given,

r = 5.

Since the centre lies on x – axis.

k = 0.

⸫Centre of circle = (h, k) = (h, 0)

The equation of the circle in given by,

(x – h)² + (y – k)² = r²

(x – h)² + (y – 0)² = (5)²

(x – h)² + y² = 25--------(i)

Since the curie parses through the point (2, 3),

Putting x = 2 and y = 3 in equation (1), We get.

(2 – h)² + (3)² = 25

2² + h² – 22.h + 9 = 25

4 + h²– 4h + 9 = 25

h² – 4h + 13 – 25 = 0

h² – 4h – 12 = 0

h² – (6 – 2)h – 12 = 0

h² – 6h + 2h – 12 – 0

h(h – 6) + 2(h – 6) = 0

(h – 6)(h + 2) = 0

h = 6 and h = –2

When h = 6,

From (i), Equation of circle is,

(x –6)² + y² = 25

(x – 6)² + (y – 0)² = 52

When h = –2,

Equation of circle is, (x + 2)² + (y – 0)² = 5² or x² $\mathrm{<br>}{}_2+y^2+4x-21=0$

 

Q13. Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes.

A.13. Let the equation of the circle be,

(x – h)² + (y – k)² = r² – 0-----(i)

As the circle is passing through (0, 0) we get,

(0 – h)² + (0 – k)² = r²

(–h)² + (–k)² = r²

h² + k² = r²--------(ii)

The circle also makes intercepts a and b on the cooperate axes.

Let intercept on x–axis be 'a' and on y–axis be 'b'

⸫Circle also passes through (a, 0) and (0, b)

Putting x = a and y = 0 in (i)

(a – h)² + (0 – k)² = r²

a² + h² – 2.a.h + (–k)² = r²

a² – 2ah + h² + k² = r²

Putting value of r² from (ii), we get

a² – 2ah + h² + k² = h² + k²

a² = 2ah

a = 2h

h =  $\frac{a}{2}$

Putting x = 0 andy = b in (i).

(0 – h)² + (b – k)² = r²

h² + b² + k² – 2bk = r²

Putting value of r² from (ii),

h² + b² + k² – 2bk = h² + k²

b² = 2bk

b = 2k

k =  $\frac{b}{2}$

Putting values of h and k in (ii),

${\left(\frac{a}{2}\right)}^2+{\left(\frac{b}{2}\right)}^2=r^2$

$\frac{a^2}{4}+\frac{b^2}{4}=r^2$

r² = $\frac{a^2+b^2}{4}$

Putting the values of h₁ k and r² in (i),

${\left(x-\frac{a}{2}\right)}^2+{\left(y-\frac{b}{2}\right)}^2=\frac{a^2+b^2}{4}$

x² + $\frac{a^2}{4}$ – 2.x.  $\frac{a}{2}$ + y² +  ${\left(\frac{b}{2}\right)}^2$ – 2 .y.  $\frac{b}{2}$ =  $\frac{a^2+b^2}{4}$

x² + $\cancel{\frac{a^2}{4}}$ – ax + y² +  $\cancel{\frac{b^2}{4}}$ – yb =  $\cancel{\frac{a^2}{4}}+\cancel{\frac{b^2}{4}}$

⸫The equation of the circle is,

x² – ax + y² – by = 0

 

Exercise 11.2

In each of the following Exercises 1 to 6, find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.

Q1. y² = 12x

A.1. y² = 4ax

Comparing with the given equation, y² = 12x,

We get, 4a = 12

a =  $\frac{12}{4}=3$

⸫Co–ordinates of the focus are (a, 0) = (3, 0)

Axis of Parabola : x-axis.

Equation, of directrix as, x = –a

x = –3

Length of latus rectum = 4a

= 4 × 3

= 12

 

Q2. x² = 6y

A.2. x² = 4ay.

Comparing with the given equation x² = 6y

We get,

4a = 6

a =  $\frac{6}{4}=\frac{3}{2}$

Co–ordinates of focus are (0, a) =  $\left(0,\frac{3}{2}\right)$

Axis of Parabola : y-axis.

Equation of directrix is,

y = –a

y = –  $\frac{3}{2}$

Length of latus rectum =4a

= 4 ×  $\frac{3}{2}$

= 2 × 3

= 6.

 

Q3. y² = –8x

A.3. y² = –4ax

Comparing with the given equation y² = –8x

We get,

–4ax = –8x

a =  $\frac{8}{4}=2$

⸫ Co–ordinates of focus is (–0, 0) = (–2, 0)

Axis of Parabola : x-axis.

Equation of directrix is,

x = a

x = 2

Length of latus rectum =4a

= 4 × 2 = 8

 

Q4.x² = –16y

A.4. x² = –4ay

Comparing with the given equation x² = –16y

We get, –4a = –16

a =  $\frac{-16}{-4}$

a = 4

Co–ordinate of focus is (0, –a)

= (0, –4)

Axis of Parabola : y-axis.

Equation of directrix is

y = a

y = 4

Length of latus rectum =4a

= 4 × 4

= 16

 

Q5. y² = 10x

A.5. y² = 4ax

Comparing with the given equation y² = 10x,

We get,

4a = 10

a =  $\frac{\cancel{10}5}{\cancel{4}2}$

a =  $\frac{5}{2}$

⸫ Co–ordinates of focus is (a, 0) =  $\left(\frac{5}{2},0\right)$

Axis of Parabola : x-axis.

Equation of directrix is.

x = –a

x =  $-\frac{5}{2}$

Length of latus rectum =4a

=  $\mathrm{4\text{'}}<br>\frac{5}{2}$

= 2 × 5

= 10.

 

Q6.x² = –9y

A.6. The given equation involves x², so its axis is y–axis.

Also the Co–efficient of y is negative.

Hence we use the equation,

x² = –4ay

Comparing with the given equation x² = –9y,

We get,

–4a = –9

a =  $\frac{-9}{-4}$

a =  $\frac{9}{4}$

Co–ordinates of focus in (0, –a) =  $\left(0,-\frac{9}{4}\right)$

Axis of Parabola : y-axis.

equation of directrix is,

y = a

y =  $\frac{9}{4}$

Length of latus rectum =4a

= 4 ×  $\frac{9}{4}$

= 9

In each of the Exercises 7 to 12, find the equation of the parabola that satisfies the

given conditions:

 

Q7. Focus (6, 0); directrix x = –6.

A.7. Since the focus (6, 0) lien on the x–axis, the x–axis is the axis of parabola

Hence the equation is either y² = 4ax or y² = –4ax

Since the directrix is x = –6 and the focus (6, 0) has positive x – Coordinate,

The equation must be y² = 4ax

with a = 6

Hence, equation of parabola is,

y² = 4ax

y² = 4(6)x

y² = 24x

 

Q8. Four (0, –3); directrix y = 3.

A.8. Since the focus (0, –3) lies on the y–axis, the y–axis is the axis of parabola.

Hence the equation is either x² = 4ay or x² = –4ay

Since the directrix is y = 3 and the forces (0, –3) has negative y Co–ordinate.

The equation must be

x² = –4ay

Co–ordinate of focus = (0, –a)

(0, –a) = (0, –3)

–a = –3

a = 3

⸫ Equation of parabola is

x² = –4ay

x² = –4(3)y

x² = –12y

 

Q9. Vertex (0, 0); focus (3, 0)

A.9. Since the focus (3, 0) lies on the x-axis, the x-axis is the axis of parabola.

Hence the equation is either y² = 4ax or y² = –4ax

Since the focus has positive x co-ordinate,

The equation must be y² = 4ax

Co-ordinate of focus (a, 0) = (3, 0)

a = 3

⸫ The equation is given by

y² = 4(3)x

y² = 12x

 

Q10. Vertes (0, 0); focus (–2, 0)

A.10. Focus (-2, 0) lies on x-axis and the x-Co-ordinate is negative.

The equation must be, y² = 4ax

Co-ordinate of focus = (–a, 0) = (–2, 0)

–a = –2

a = 2

⸫ Equation of a parabola is,

y² = –4(2)x

y² = –8x

 

Q11. Vertex (0, 0) passing through (2, 3) and axis is along x-axis

A.11. Since the axis of parabola is x-axis,

The equation parabola is either y² = 4ax or y² = 4ax.

Also it passes through (2, 3) which lies in the first quadrant.

So the equation is,

y²= 4ax

Putting x = 2 and y = 3, we set

(3)² = 4(a) (2)

a =  $\frac{9}{8}$

⸫ The equation of parabola is y² = 4 $\times \frac{9}{8}x$

y² = $\frac{9}{2}x$

2y² = 9x

 

Q12. Vertex (0, 0) passing through (5, 2) and symmetric with respect to y-axis

A.12. Since the parabola is symmetric with respect to y-axis and has vertex (0, 0)

The equation in of the form x³ = 4ay or x² = 4ay.

The parabola passes through (5, 2) which lies on the 1st quadrant

⸫ The equation of parabola is of the form,

x² = 4ay

Putting x = 5 and y = 2,

(5)² = 4(a) (2)

25 = 8a

a =  $\frac{25}{8}$

⸫ The equation of the parabola is,

x² = 4ay

$\Rightarrow x^2=4\left(\frac{25}{8}\right)y$

$\Rightarrow x^2=\frac{25}{2}y$

2x² = 25y,