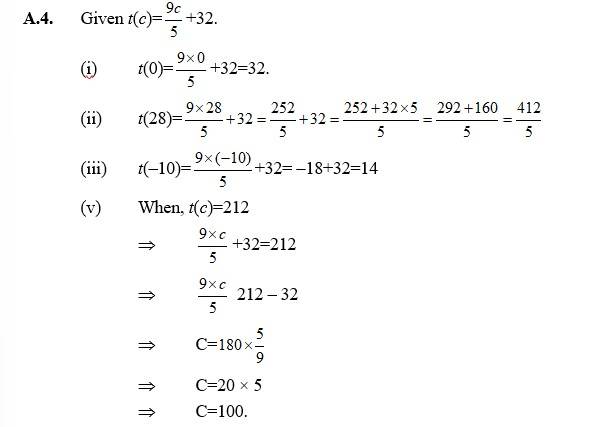Class 11 Maths NCERT Solutions Chapter 2 Relations and Functions: Topics, Questions, Preparation

Exercise 2.1

 

Q2. If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A×B).

A.2. Given, n(A) = 3

n(B) = 3 or B = {3,4,5}

So, number of elements in A× B = n(A× B) = n(A)× n(B) = 3 ×3 = 9.

 

Q3. If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.

A.3. Given, G = {7, 8} and H = {5, 4, 2}

By the definition of the Cartesian product,

G ×H = {(x, y): x∈G and y = ∈ H}

= {((7, 5), (7, 4), (7, 2), (8, 5),(8,4), (8,2)}

H× G = {(x, y): x∈ H and y ∈G}

= {(5, 7), (5, 8), (4,7), (4, 8), (2, 7), (2,8)}

 

Q4. State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.

(i) If P = {m, n} and Q = { n, m}, then P × Q = {(m, n),(n, m)}.

(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x  $\in$ A and y  $\in$ B.

(iii) If A = {1, 2}, B = {3, 4}, then A ×  $($  B   ∩   ϕ   )   =   ϕ  .

A.4. (i) False. Here P = {m, n}, n(p)=2

Q = {n, m}, n(Q)=2

n(P× Q) = n(P)× n(Q) = 2× 2 = 4.

So, P ×Q = {((m, n),(m, m),(n, n),(n, m)}

(ii) True.

(iii) True. { A ×(B   ∩   ϕ ) = A× ϕ  . { ∵ B ∩   ϕ = ϕ   }

= n(A) ×0 {∵ ϕ   is empty set}

= ϕ  

 

Q5. If A = {–1, 1}, find A × A × A.

A.5. Given, A = {1,1}

So, A× A = {(1,1),(1,1),(1,1),(1,1)}

A ×A ×A = {(1,1),(1,1),(1,1),(1,1)} ×{1,1}

= {(1,1.1),(1, 1, 1),(1, 1, 1,),(1,1,1), (1,1,1), (1, 1,1), (1, 1,1), (1,1,1)}

 

Q6. If A × B = {(a, x),(a , y), (b, x), (b, y)}. Find A and B.

A.6. Given,

A ×B = {(a, x),(a, y),(b, x),(b, y)}

We know that,

A ×B = {(p, q); p ∈ A and q ∈ B}

So, A = {a, b} and B = {x, y}.

 

Q7. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that (i) A × (B∩ C) = (A × B)∩ (A × C). (ii) A × C is a subset of B × D.

A.7.Given,

A={1, 2}, B = {1,2,3,4}, C={5,6} and D={5,6,7,8}

(i)L.H. S = A ×(B∩ C) = {1,2} [{1,2,3,4} ∩{5,6}]

={1,2}× ϕ  

= ϕ  .

R.H.S = (A× B)∩ (A ×C)=[{1,2}×{1,2,3,4}]∩[{1,2} {5,6}]

=[{(1 , 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)]∩ [{1,5),(1,6),(2,5), (2,6)}]

= ϕ  .

Hence, L.H.S= R.H.S.

(ii)

A× C ={1, 2}× {5,6}

={(1,5),(1,6),(2,5),(2,6)}

B× D ={1,2,3,4} ×{5,6,7,8}

={(1,5),(1,6),(1,7),(1,8),(2,5),(2,6),(2,7),(2,8),(3,5),(3,6),(3,7),(3,8),(4,5),(4,6),(4,7),(4,8)}

As every element of A C is also an element of B× D.

A ×C  $\subset$ B ×D

 

Q8. Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.

A.8. A Given, A={1,2}

B={3,4}

So, A× B={(1,3),(1,4),(2,3),(2, 4)}

i.e., n(A ×B)=4

A ×B will have subset =2⁴=16.They are,

Φ,{(1,3)},{(1,4)},{(2, 3)},{(2,4)},{(1,3),(1,4)},{(1,3),(2,3)},

{(1,3),(2, 4)},{(1,4),(2, 3)},{(1,4),(2, 4)}, {(2,3),(2, 4)},

{(1,3),(1,4),(2, 3)},{(1,3),(1,4),(2,4)}, {(1,3),(2,3),(2, 4)},{(1,4),(2,3),(2,4)},

and {(1,3),(1,4),(2,3),(2,4)}

 

Q9. Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.

A.9. Given, n(A)=3

n(B)= 2

So, n(Ax B)=n(A).n(B)=3x 2=6

as (x, 1),(y, 2),(z, 1) ∈Ax B={(x, y), x∈Aand y∈B}.

A={x, y, z} and B={1,2}

As n(A) = 3as n(B) = 2

 

Q10. The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0,1). Find the set A and the remaining elements of A × A.

A.10. Given, n(A × A)=9

n(A) ×n(A) = 9.

n(A)² = 3².

n(A) = 3 .

And (–1,0),(0,1)  $\in$ A × A i.e., A × A = {(x, y), x  $\in$ A, y  $\in$ B}

⸫A={–1,0,1}

And A × A={–1,0,1} × {–1,0,1}

={(–1, –1),( –1,0),( –1,1),(0, –1),(0,0),(0,1),(1, –1),(1,0),(1,1)}

 

Exercise 2.2

 

Q1. Let A = {1, 2, 3,...,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y $\in$ A}. Write down its domain, co domain and range.

A.1. Given,A ={1,2,3, …, 14}

R ={(x, y): 3x – y = 0; x, y  $\in$ A}

={(x, y): 3x = y; x, y  $\in$ A}.

= {(1,3),(2,6),(3,9),(4,12)}

Domain of R is the set of all the first elements of the ordered pairs in R

So, domain of R={1,2,3,4}

Codomain of R is the whole set A.

So, codomain of R={1,2,3, …, 14}

Range of R is the set of all the second elements of the ordered pains in R.

So, range of R={3,6,9,12}

 

Q2. Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y $\in$ N}. Depict this relationship using roster form. Write down the domain and the range.

A.2. Given,R ={(x, y): y = x + 5, x is a natural number less than 4; x, y $\in$ N}

={(x, y): y = x + 5; x, y  $\in$ N and x < 4}.

={(1,1+5), (2,2+5), (3,3+5)}

={(1,6), (2,7), (3,8)}

So, domain of R = {1,2,3}

range of R = {6,7,8}

 

Q3. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x $\in$ A, y  $\in$ B}. Write R in roster form.

A.3. Given,A={1,2,3,5}

B={4,6,9}

R={(x, y) : the difference of x & y is odd; x  $\in$ A, y  $\in$ B}.

={(x, y):|x – y| is odd and x  $\in$ A, y  $\in$ B}

={(1,4),(1,6),(2,9),(3,4),(3,6),(5,4),(5,6)}.

Q4. The Fig 2.7 shows a relationship between the sets P and Q. Write this relation

(i) in set-builder form (ii) roster form. What is its domain and range?

A.4. As R is a relation from set P to Q.

(i)R = {(x, y): x – 2 = y ; 5 ≤ x ≤ 7}

(ii)R = {(5,3),(6,4),(7,5)}

Domain of R={5,6,7}

range of R={3,4,5}

 

Q5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a , b $\in$ A, b is exactly divisible by a}.

(i) Write R in roster form

(ii) Find the domain of R

(iii) Find the range of R.

A.5. Given, A={1,2,3,4,6}

R={(a, b): a, b  $\in$ A, b is exactly divisible by a}

(i)R={(1,1),(1,2),(1,3),(1,4),(1,6),(2,2),(2,4),(2,6), (3,3),(3,6),(4,4),(6,6)}

(ii)Domain of R={1,2,3,4,6}

(iii)Range of R={1,2,3,4,6}

 

Q6. Determine the domain and range of the relation R defined by R = {(x, x + 5) : x $\in$ {0, 1, 2, 3, 4, 5}}.

A.6. Given,R ={(x, x+5): x $\in$ {0,1,2,3,4,5}}

={(0,0+5), (1,1+5), (2,2+5), (3,3+5), (4,4+5), (5,5+5)}

={(0,5),(1,6),(2,7),(3,8),(4,9),(5,10)}

So, domain of R={0,1,2,3,4,5}

range of R={5,6,7,8,9,10}

 

Q7. Write the relation R = {(x,x³) : x is a prime number less than 10} in roster form.

A.7. GivenR={(x, x³) : x is a prime number less than 10}

R ={(x, x³) : x = 2,3,5,7}

={(2,2³),(3,3³),(5,5³),(7,7³)}

={(2,8),(3,27),(5,125),(7,343)}

 

Q8. Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.

A.8. Given, A={x, y, z}so, n(A)=3

B={1,2} so n(B)=2

⸫ n(A × B)=n(A) ×n(B)=3 × 2=6

Hence, no. of relation from A to B=Number of subsets of A × B

=2⁶

=64.

 

Q9. Let R be the relation on Z defined by R = {(a,b): a, b $\in$ Z, a – b is an integer}. Find the domain and range of R.

A.9. Given,R={(a, b): a, b $\in$ z and a – b is an integer}

We know that, the difference of two integers is also an integer.

R={(a, b): a – b  $\in$ z & a, b  $\in$ z}

Domain of R=Z.

Range of R= Z.

 

Exercise 2.3

Q1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.

(i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}

(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}

(iii) {(1,3), (1,5), (2,5)}.

A.1. (i)Domain of the given relation ={2,5,8,11,14,17}

Since every element of the domain has one and only one image, the given relation is a fxⁿ.

So, domain ={2,5,8,11,14,17}

range ={1}

(ii)Domain of the given relation ={2,4,6,8,10,12,14}

Since every element of the domain has one and only one image, the given relation is a fxⁿ.

So, domain = {2, 4, 6, 8, 10, 12, 14}

range ={1,2,3,4,5,6,7}

(iii)Domain of the given relation ={1,2}

As element 1 has more than one image i.e., 3 and 5, the given relation is not a fxⁿ.

 

Q3. A function f is defined by f(x) = 2x –5. Write down the values of

(i) f (0), (ii) f (7), (iii) f (–3).

A.3. Give, f(x) = 2x – 5.

(i)f(0)=(2 × 0) –5=0 – 5= –5

(ii)f(7)=(2 × 7) –5=14 – 5=9

(iii)f(–3)=2 ×(–3) –5= –6 – 5= –11.

 

Q4. The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C) = $\frac{9}{}$  C / 5   +   3   2  .

Find (i) t(0) (ii) t(28) (iii) t(–10) (iv) The value of C, when t(C) = 212.

 

 

Q5. Find the range of each of the following functions.

(i) f (x) = 2 – 3x, x  $\in$ R, x > 0.

(ii) f (x) = x²+ 2, x is a real number.

(iii) f (x) = x, x is a real number.

A.5. (i)f(x)=2 – 3x, x $\in$ R, x>0.

Given, x>0

3x>3 × 0

3x>0

(–1) × 3x<(–1) × 0.

–3x<0

2 – 3x<0+2

2 – 3x<2

i.e., f(x) < 2

Hene, range of f(x) = (– ꝏ, 2)

(ii)Given, f(x) = x²+2, x is a real number.

Since, x is a real number,

x² ≥ 0 (x²=0 for x=0)

x²+2 ≥ 0+2

x²+2 ≥ 2

f(x) ≥ 2

⸫Range of f(x) = [2, ꝏ) 

(iii)Given, f(x) = x, x is a real number.

As, f(x) = x, the range of f(x) is also real.

i.e., Range of f(x) = R.

 

Miscellaneous

f(x) ≥ 0

So, range of f(x)=[0, ꝏ)

 

Q5. Find the domain and the range of the real function f defined by $f$  (   x   )   =   |   x   −   1   |  .

A.5. Given, f(x)=|x – 1|.

The given function is defined for all real number x.

Hence, domain of f(x)=R.

As f(x)=|x – 1|, x  $\in$ R is a non-negative no.

Range of f(x)=[0, ꝏ), if positive real numbers.

 

Q7. Let f, g : R→R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and $\frac{f}{}$  g  .

A.7. Given, f(x) = x+1. and g(x) = 2x – 3.

So, (f +g)(x) = f(x)+g(x) = (x+1)+(2x – 3) = x+1+2x – 3 = 3x – 2

(f – g)(x) = f(x) –g(x) = (x+1)–(2x–3) = x+1 – 2x+3 = 4 – x

$\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}=\frac{x+1}{2x-3} such that x\ne \frac{3}{2}$

 

Q8. Let f = {(1,1), (2,3), (0,–1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.

A.8.  Given, f(x) = (ax + b)

= {(1,1),(2,3),(0, – 1),(–1, –3)} .

As (1,1)  $\in$ f.

Then, f(1)=1   [⸪ f(x) = y for (x, y)]

a × 1+b=1

a+b=1…… (1)

and (0, – 1)  $\in$ f .

Then, f(0)= –1

a× 0+b= –1

b= –1……..(2)

Putting value of (2) in (1) we gets

a – 1=1

a=1+1

a=2

So, (a, b)=(2, –1)

 

Q9. Let R be a relation from N to N defined by R = {(a, b) : a, b $\in$ N and a = b²}. Are the following true?

(i) (a,a)  $\in$ R, for all a _ N (ii) (a,b)  $\in$ R, implies (b,a)  $\in$ R

(iii) (a,b)  $\in$ R, (b,c)  $\in$ R implies (a,c)  $\in$ R.

Justify your answer in each case.

A.9. Given, R={(a, b): a, b  $\in$ N and a = b²}

(i)Let a = 2  $\in$ N

Then b = 2² = 4 $\in$ N

but a ≠ b.

Hence the given statement is not true.

(ii)For a=b² the inverse b=a² may not hold true

Example (4,2)  $\in$ R, a=4, b=2 and a=b²

but (2,4)  $\notin$ R.

Hence, the given statement is not true.

(iii)If (a,b)  $\in$ R

a=b²……(1)

and (b, c)  $\in$ R

b=c²…….(2)

so for (1) and (2),

a=(c²)²=c⁴.

is, a ≠c²,

Hence, (a, c)  $\notin$ R.

⸫The given statement is false.

Q10. Let A ={1,2,3,4}, B = {1,5,9,11,15,16} and f = {(1,5), (2,9), (3,1), (4,5), (2,11)} Are the following true?

(i) f is a relation from A to B (ii) f is a function from A to B.

Justify your answer in each case.

A.10. Given,

A={1,2,3,4}

B={1,5,9,11,15,16}

f={(1,5),(2,9),(3,1),(4,5),(2,11)}.

(i)As every element of f is an element of A × B

We can clearly say that f  $\subset$ A × B.

⸫f is a relation from A to B.

(ii)As the element 2 of the domain has two image i.e., 9 and 11. f is not a function.

 

Q11. Let f be the subset of Z × Z defined by f = {(ab, a + b) : a, b _ Z}. Is f a function from Z to Z? Justify your answer.

A.11. Given, f={(ab, a+b): a, b $\in$ z}

Let a=1 and b=1;                   a, b $\in$ z.

So, ab=1 × 1=1

a+b=1+1=2.

So, we have the order pair (1,2).

Now, let a= –1 and b= –1; a, b  $\in$ z

So, ab=(–1) × (–1)=1

a+b=(–1)+(–1)= –2

So, the ordered pair is (1, –2).

⸫The element 1 has two image i.e., 2 and –2.

Hence, f is not a function.

 

Q.12. Let A = {9,10,11,12,13} and let f : A→N be defined by f (n) = the highest prime factor of n. Find the range of f.

A.12. Given, A={9,10,11,12,13}.

f(x)=the highest prime factor of n.

and f: A → N.

Then, f(9)=3 [⸪ prime factor of 9=3]

f (10)=5 [⸪ prime factor of 10=2,5]

f(11)=11 [⸪ prime factor of 11 = 11]

f(12)=3 [⸪ prime factor of 12 = 2, 3]

f(13)=13 [⸪ prime factor of 13 = 13]

⸫Range of f=set of all image of f(x) = {3,5,11,13}.