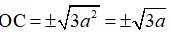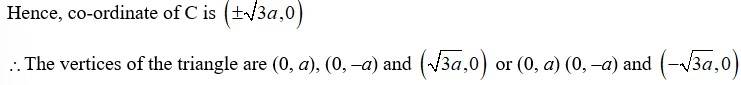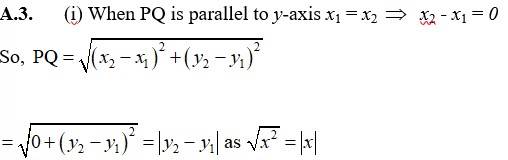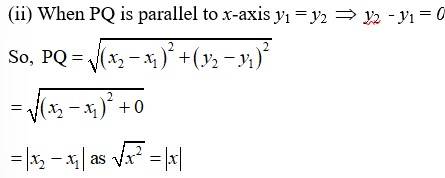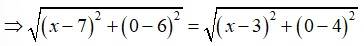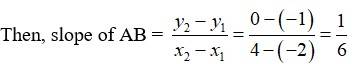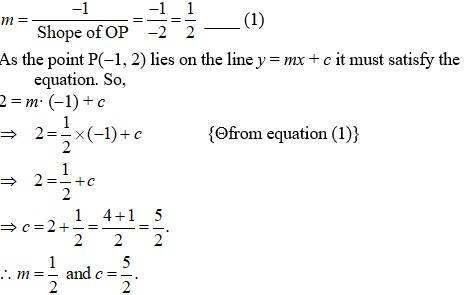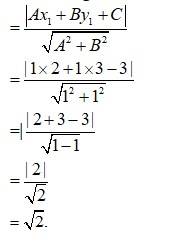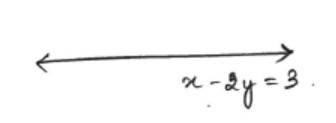NCERT Solutions for Class 11 Maths Chapter 10 Straight Lines: Overview, Questions, Preparation

Exercise 10.1

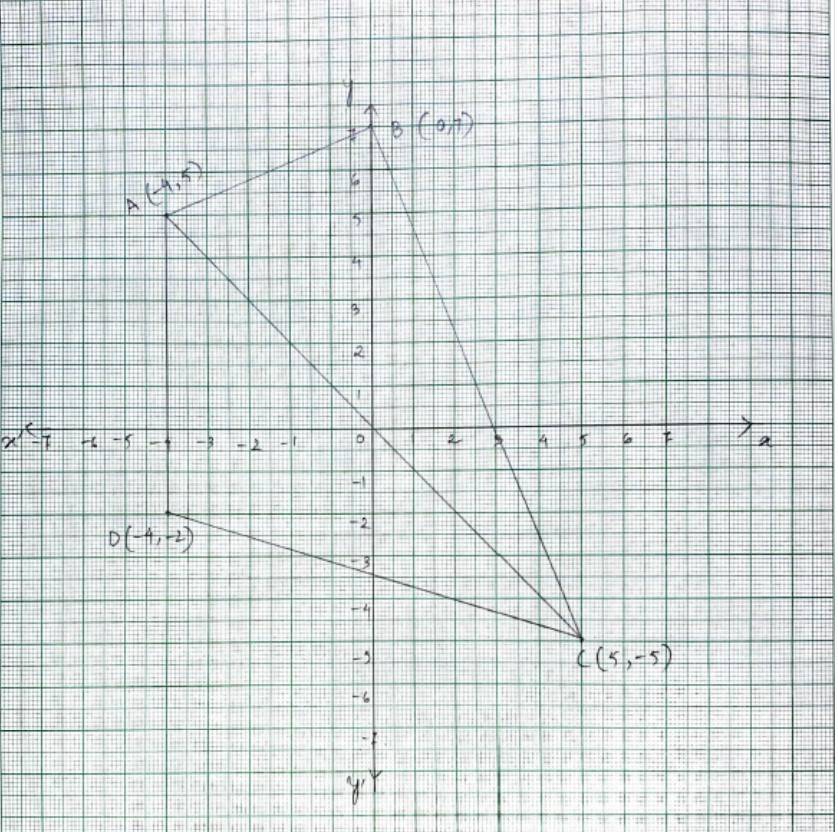
Q1. Draw a quadrilateral in the Cartesian plane, whose vertices are (– 4, 5), (0, 7),

(5, – 5) and (– 4, –2). Also, find its area.

A.1. Let the given points be A(–4, 5), B(0, 7), C(5, –5) and D(–4, –2).

Then quadrilated ABCD can be plotted on the graph by joining the points A, B, C and D.

We connect diagonal AC such that

area (ABCD) = (ΔABC) + (ΔADC)

Now,

$\left(\Delta ABC\right)=\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|$

$=\frac{1}{2}\left|-4\left[7-\left(-5\right)\right]+0\left[-5-5\right]+5\left[5-7\right]\right|\text{\hspace{0.17em}unit}{}^2$

$=\frac{1}{2}\left|-4\left(7+5\right)+0+5\left(5-7\right)\right|\text{\hspace{0.17em}unit}{}^2$

$=\frac{1}{2}|\left(-4\right)\times 12+5\times \left(-2\right)|unit{}^2$

$=\frac{1}{2}|-48-10|unit{}^2$

$=\frac{1}{2}\left|-58\right|\text{\hspace{0.17em}unit}{}^2$

$=\frac{58}{2}\text{unit\hspace{0.17em}}{}^2=29\text{\hspace{0.17em}unit}{}^2$

Similarly,  $\left(\Delta ACD\right)=\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|$

$=\frac{1}{2}\left|-4\left[-5-\left(2\right)\right]+5\left[-2-5\right]+\left(-4\right)\left[5-\left(-5\right)\right]\right|\text{\hspace{0.17em}unit}{}^2$

$=\frac{1}{2}|-4\left(-5+2\right)+5\left(-2-5\right)-4\left(5+5\right)|unit{}^2$

$=\frac{1}{2}|\left(-4\right)\times \left(-3\right)+5\times \left(-7\right)-4\times \left(10\right)|unit{}^2$

$=\frac{1}{2}|12-35-40|unit{}^2$

$=\frac{1}{2}\left|-63\right|\text{\hspace{0.17em}unit}{}^2$

$=\frac{63}{2}\text{\hspace{0.17em}unit}{}^2$

Hence, area (ABCD) =  $29+\frac{63}{2}\text{\hspace{0.17em}unit}{}^2$

$=\frac{58+63}{2}\text{\hspace{0.17em}unit}{}^2=\frac{121}{2}\text{\hspace{0.17em}unit}{}^2$

 

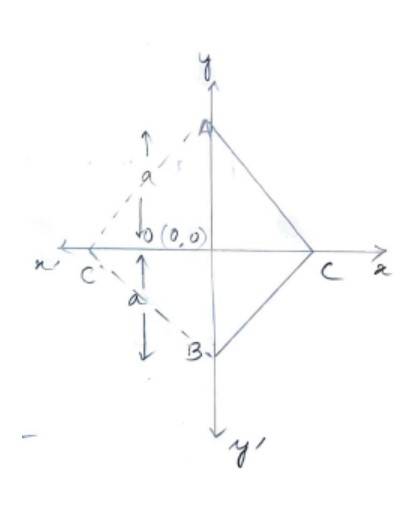
Q2. The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.

A.2. Let ABC be the equilateral triangle of side 2a and 0 be the origin. Then

AB = BC = AC = 2a

O is the mid-point of AB we have AO = a

BO = a

We know that A and B lies on y-axis so they have co-ordinate of the form (0, y).

Hence, co-ordinate of A is (0, a) and that of B is (0, –a)

Since OC, bisects AB at right angle, by Pythagoras theorem,

AC²= OA² + OC²

$\Rightarrow {\left(2a\right)}^2={\left(a\right)}^2+OC{}^2$

$\Rightarrow OC{}^2=4a^2-a^2$ $$

And as C we on x-axis it has co-ordinate of the form (x, 0)

 

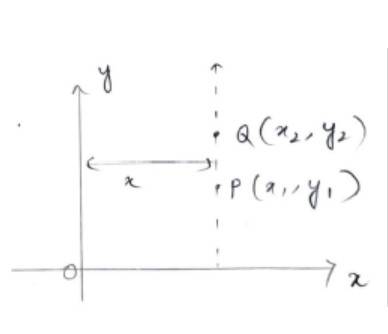
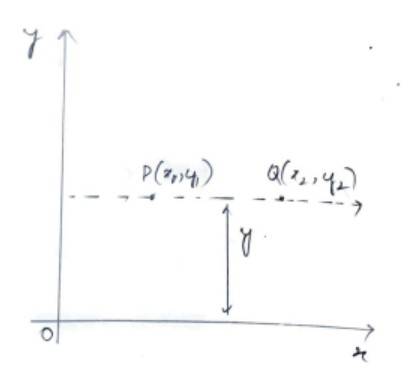
Q3. Find the distance between P (x1, y1) and Q (x2, y2) when : (i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.

 

Q4. Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).

A.4. Let A(x, 0) be the point on x-axis when is equidistant from P(7, 6) and Q(3, 4)

Then, PA = QA $<br>$

Squaring both sides, we get,

$\Rightarrow x^2-14x+49+36=x^2-6x+9+16$

$\Rightarrow 49+36-9-16=14x-6x$

$\Rightarrow 60=8x$

$\Rightarrow x=\frac{60}{8}=\frac{15}{2}$

$\therefore$ The required point on x-axis is  $\left(\frac{15}{2},0\right).$

 

Q5. Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, – 4) and B (8, 0).

A.5. Let 0(0, 0) be the origin and A be the mid-point of line joining P(0, –4) and B(8, 0)

Then, co-ordinate of A =  $\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)=\left(\frac{0+8}{2},\frac{-4+0}{2}\right)=\left(4,-2\right)$

$\therefore$ Slope of OA, m =  $\frac{y_2-y_1}{x_2-x_1}=\frac{-2-0}{4-0}=-\frac{2}{4}=\frac{-1}{2}$

 

Q6. Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.

A.6. Let the given point be A(4, 4), B(3, 5) and C(–1, –1)

Then, slope of AB, m₁ = $\frac{5-4}{3-4}=\frac{1}{-1}=-1$

Slope of AC, m₂ = $\frac{-1-4}{-1-4}=\frac{-5}{-5}=1$

And slope of BC, m₃ = $=\frac{-1-5}{-1-3}=\frac{-6}{-4}=\frac{3}{2}$

As m₁ – m₂ = –1 × 1 = –1

$\Rightarrow m_1=\frac{-1}{m_2}$

We conclude that AB and AC are perpendicular to each other.

Hence, ABC is a right-angle triangle right-angled at A

 

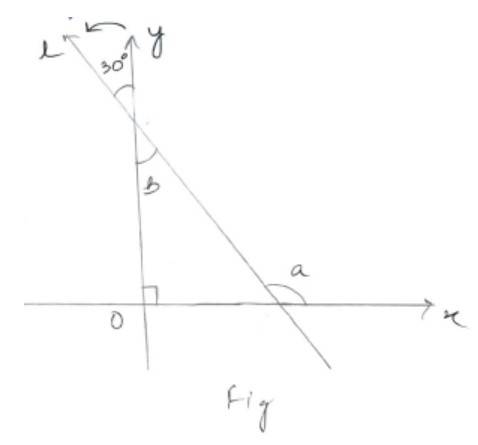
Q7. Find the slope of the line, which makes an angle of 30°with the positive direction of y-axis measured anticlockwise.

A.7. Let l be the line making 30° with y-axis as shown in figure. Then,

Angle a =  $\angle b$ + 90° (Sum of exterior angle of a triangle)

$\Rightarrow \angle a=30°+90°$ (  $30°=\angle b$ vertically opposite angle)

$\Rightarrow \angle a=120°$

So, slope of line l = tan a

= m = tan 120°

= tan(180° – 60°)

= –tan 60°

$=-\surd 3$

 

Q8. Find the value of x for which the points (x, – 1), (2,1) and (4, 5) are collinear.

A.8. Let P(x, –1), Q(2, 1) and R(4, 5) be the collinear points. Then,

Slope of PQ = Slope of QR

$\Rightarrow \frac{1-\left(-1\right)}{2-x}=\frac{5-1}{4-2}$

$\Rightarrow \frac{1+1}{2-x}=\frac{4}{2}$

$\Rightarrow 2\times 2=4\left(2-x\right)$

$\Rightarrow 4=8-4x$

$\Rightarrow x=\frac{4}{4}$

$\Rightarrow x=1$

 

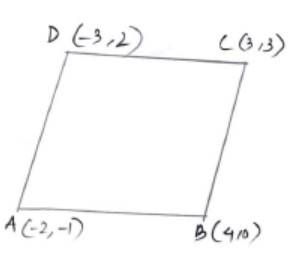
Q9. Without using distance formula, show that points (– 2, – 1), (4, 0), (3, 3) and (–3, 2) are the vertices of a parallelogram.

A.9. Let A(–2, –1), B(4, 0), C(3, 3) and D(–3, 2) be the given points.

Slope of DC =  $\frac{3-2}{3-\left(-3\right)}=\frac{1}{3+3}=\frac{1}{6}$

As slope of AB = slope of DC

We conclude that AB | | DC.

Similarly, slope of BC =  $\frac{3-0}{3-4}=\frac{3}{-1}=-3$

Slope of AD =  $\frac{2-\left(-1\right)}{-3-\left(-2\right)}=\frac{2+1}{-3+2}=\frac{3}{-1}=-3$

As slope of BC = slope of AD we conclude that BC | | AD.

Hence, as the pair of opposite sides of ABCD are parallel we can conclude that the given points are the vertices of a parallelogram.

 

Q10. Find the angle between the x-axis and the line joining the points (3,–1) and (4,–2).

A.10. Slope of line joining points A(3, –1) and B(4, –2) is

$m=\frac{-3-\left(-1\right)}{4-3}=\frac{-2+1}{1}=-1$

As slope of AB is the angle made by the line-segment AB w.r.t. x-axis, the angle between them is  $$ and is given by  $ta\mathrm{n\Theta }=m$

$\Rightarrow ta\mathrm{n\Theta }=-1\Rightarrow ta\mathrm{n\Theta }=-tan45°=tan\left(180°-45°\right)$

$\Rightarrow tan=tan135°$

$\Rightarrow =135°$

 

Q11. The slope of a line is double of the slope of another line. If tangent of the angle between them is  $\frac{1}{3}$ , find the slopes of the lines.

A.11. Let the two slopes be m and 2m. And if  Θ $$ is the angle between the two lines.

$ta\mathrm{n\Theta }=\left|\frac{m_1-m_2}{1+m_1{m}_2}\right|$

$\Rightarrow \frac{1}{3}=\left|\frac{2m-m}{1+2m..m}\right|=\left|\frac{m}{1+2m^2}\right|$

$\Rightarrow \frac{m}{1+2m^2}=\pm \frac{1}{3}\left(\because \left|x\right|=\pm x\right)$

Case I. When  $\frac{m}{1+2m}=\frac{1}{3}$

$\Rightarrow 3m=2m^2+1$

$\Rightarrow 2m^2-3m+1=0$

$\Rightarrow 2m^2-2m-m+1=0$

$\Rightarrow 2m\left(m-1\right)-\left(m-1\right)=0$

$\Rightarrow \left(m-1\right)\left(2m-1\right)-0$

$\Rightarrow m=1m=\frac{1}{2}$

Case II. When  $\frac{m}{1+2m^2}=-\frac{1}{3}$

$\Rightarrow 3m=-\left(1+2m^2\right)$

$\Rightarrow 3m=-1-2m^2$

$\Rightarrow 2m^2+3m+1=0$

$\Rightarrow 2m^2+2m+m+1=0$

$\Rightarrow 2m\left(m+1\right)+\left(m+1\right)=0$

$\Rightarrow \left(m+1\right)\left(2m+1\right)=0$

$\Rightarrow m=-1m=-\frac{1}{2}$

Hence,  $m=1,\frac{1}{2},-1m=-\frac{1}{2}$

$\therefore$ The possible slopes of the two lines (m, 2m) are (1, 2),  $\left(\frac{1}{2},1\right),\left(-1,-2\right)$ and  $\left(-\frac{1}{2},-1\right).$

 

Q12. A line passes through (x₁, y₁) and (h, k). If slope of the line is m, show that k – y₁ = m (h – x₁).

A.12. Let the line l passes through points (x₁, y₁) and (h, x)

Then slope of l,

$m=\frac{k-y_1}{h-x_1}$

$\Rightarrow \left(h-x_1\right)m=k-y_1$

Hence, proved

 

Q13. If three points (h, 0), (a, b) and (0, k) lie on a line, show that  $\frac{a}{h}+\frac{b}{k}=1$ .

A.13. Since the three points say P(h, o), Q(a, b) and R(o, k) lie on a line.

Slope of PQ = slope of QR

$\Rightarrow \frac{b-o}{a-h}=\frac{k-b}{o-a}$

$\Rightarrow \frac{b}{a-h}=\frac{k-b}{-a}$

$\Rightarrow -ab=\left(k-b\right)\left(a-h\right)$

$\Rightarrow -ab=ka-kh-ab+bh$

$\Rightarrow ka+bh=kh$

Dividing both sides by kh we get,

$\Rightarrow \frac{ka}{kh}+\frac{bh}{kh}=\frac{kh}{kh}$

$\Rightarrow \frac{a}{h}+\frac{b}{k}=1$

 

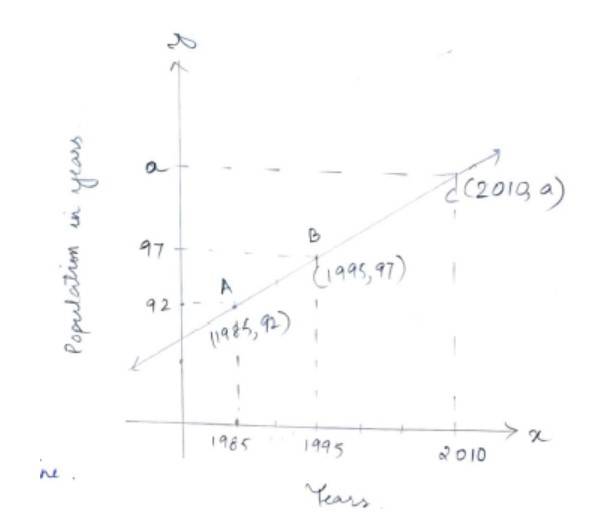
Q14. Consider the following population and year graph (Fig 10.10), find the slope of the line AB and using it, find what will be the population in the year 2010 ?

A.14. From figure,

Slope of AB =  $\frac{97-92}{1995-1985}$

$=\frac{5}{10}$

$=\frac{1}{2}$

As, A, B and C lie on same line

Slope of AB = Slope of BC

$\Rightarrow \frac{1}{2}=\frac{a-97}{2010-1995}=\frac{a-97}{15}$

$\Rightarrow 15=2\left(a-97\right)$

$\Rightarrow 15=2a-194$

$\Rightarrow 194+15=2a$

$\Rightarrow 209=2a$

$\Rightarrow a=\frac{209}{2}=104.5$

Hence, population in 2010 will be 104.5 crores.

 

Exercise 10.2

In Exercises 1 to 8, find the equation of the line which satisfy the given conditions:

Q1. Write the equations for the x-and y-axes.

A.1. For any points on x-axis the y-co-ordinate or the ordinate is always 0. Hence, the x-axis have the equation y = 0.

Similarly for xy points on y-axis the x-co-ordinate or the abscissa is always 0. Hence, the y-axis have the equation x = 0.

 

Q2. Passing through the point (– 4, 3) with slope  $\frac{1}{2}$ .

A.2. Given,

$m=\frac{1}{2},\left(x_0,y_0\right)=\left(-4,3\right)$

By point slope form equation of line is

$m=\frac{y-y_0}{x-x_0}$

$\Rightarrow \frac{1}{2}=\frac{\left(y-3\right)}{x-\left(-4\right)}$

$\Rightarrow x+4=2\left(y-3\right)$

$\Rightarrow x+4=2y-6$

$\Rightarrow x-2y+4+6=0$

$\Rightarrow x-2y+10=0$

 

Q3. Passing through (0, 0) with slope m.

A.3. Given slope = m and $\left(x_0,y_0\right)=\left(0,0\right)$

By point slope from, equation of line is

$m=\frac{y-y_0}{x-x_0}$

$\Rightarrow m=\frac{y-0}{x-0}$

$\Rightarrow m=\frac{y}{x}$

$\Rightarrow mx=y$

$\Rightarrow$  $y=mx$

 

Q5. Intersecting the x-axis at a distance of 3 units to the left of origin with slope –2.

A.5. Given m = –2

x-intercept, d = –3

Using slope intercept form, equation of line is

y = m(x – d)

$\Rightarrow y=\left(-2\right)\left[x-\left(-3\right)\right]$

$\Rightarrow y=\left(-2\right)\left(x+3\right)$

$\Rightarrow y=-2x-6$

$\Rightarrow 2x+y+6=0$

 

Q6. Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30^o with positive direction of the x-axis.

A.6. The slope of the line is m = tan 30° = $\frac{1}{\mathrm{\surd 3}}$

And x-intercept, c = 2

Using slope intercept form, equation of line is

 

Q7. Passing through the points (–1, 1) and (2, – 4).

A.7. Here (x₁, y₁) = (–1, 1) and (x₂, y₂) = (2, –4)

Using two point form, equation of line is

$y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)$

$\Rightarrow y-1=\frac{-4-1}{2-\left(-1\right)}\left(x-\left(-1\right)\right)$

$\Rightarrow y-1=\frac{-5}{2+1}\left(x+1\right)$

$\Rightarrow 3\left(y-1\right)=-5\left(x+1\right)$

$\Rightarrow 3y-3=-5x-5$

$\Rightarrow 5x+3y-3+5=0$

$\Rightarrow 5x+3y+2=0$

 

Q9. The vertices of ΔPQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.

$=\left(\frac{2-2}{2},\frac{1+3}{2}\right)=\left(\frac{0}{2},\frac{4}{2}\right)$

= (0, 2)

So equation of line passing through R(4, 5) and M(0, 2) is

$y-5=\frac{2-5}{0-4}\left(x-4\right)$

$\Rightarrow y-5=\frac{-3}{-4}\left(x-4\right)$

$\Rightarrow 4\left(y-5\right)=3\left(x-4\right)$

$\Rightarrow 4y-20=3x-12$

$\Rightarrow 3x-4y+20-12=0$

$\Rightarrow 3x-4y+8=0$

 

Q10. Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).

A.10. Slope of line passing through points (2, 5) and (–3, 6) is

$m_1=\frac{-1}{m_1}=h$

$\frac{6-5}{-3-2}=\frac{1}{-5}$

So, slope of line perpendicular to line through (2, 5) and (–3, 6) is

$m_2=-\frac{1}{\left(\frac{-1}{5}\right)}=5$

$\therefore$ Equation of line with slope 5 and passing through (–3, 5) is

$\Rightarrow 5=\frac{y-5}{x-\left(-3\right)}=\frac{y-5}{x+3}$

$\Rightarrow 5\left(x+3\right)=y-5$

$\Rightarrow 5x+15-y+5=0$

$\Rightarrow 5x-y+20=0$

 

Q11. A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1: n. Find the equation of the line.

A.11. Let P(1, 0) and Q(2, 3) be the given points. Then, slope of line joining PQ,

$m_1=\frac{3-0}{2-1}=\frac{3}{1}=3$

If A divides PQ with ratio 1:n, co-ordinate of A is

$\left(\frac{m{x}_2+n{x}_1}{m+n},\frac{m{y}_2+n{y}_1}{m+n}\right)$

$=\left(\frac{1\times 2+n\times 1}{1+n},\frac{1\times 3+n\times 0}{1+n}\right)$

$=\left(\frac{2+n}{1+n},\frac{3}{1+n}\right)$

So, slope of line perpendicular to line joining points P and Q

$m_2=\frac{-1}{m_1}=-\frac{1}{3}$

Hence, equation of line passing through point A and (perpendicular to line) joining points P and Q is given by

$m_2=\frac{y-y_0}{x-x_0}$

$\Rightarrow -\frac{1}{3}=\frac{y-\left(\frac{3}{1+n}\right)}{x-\left(\frac{2+n}{1+n}\right)}$

$\Rightarrow -\frac{1}{3}=\frac{y\left(n+1\right)-3}{x\left(n+1\right)-\left(2+n\right)}$

$\Rightarrow -\left[x\left(n+1\right)-\left(2+n\right)\right]=3\left[y\left(n+1\right)-3\right]$

$\Rightarrow -x\left(n+1\right)+\left(2+n\right)=3y\left(n+1\right)-3\times 3$

$\Rightarrow x\left(n+1\right)+3\left(n+1\right)y-\left(2+n\right)-9=0$

$\Rightarrow x\left(n+1\right)+3\left(n+1\right)y-n-2-9=0$

$\Rightarrow x\left(n+1\right)+3\left(n+1\right)y-n-11=0$

 

Q12. Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).

A.12. Let the line cuts x and y axis at intercept c. Then a = b = c

Then by intercept form the equation of line is

$\frac{x}{a}+\frac{y}{b}=1$

$\Rightarrow \frac{x}{c}+\frac{y}{c}=1$

$\Rightarrow x+y=c\left(1\right)$

Since equation (1) passes through point (2, 3).

Hence 2 + 3 = c

$\Rightarrow c=5$

So, substituting value of c in equation (1) we get

$\Rightarrow x+y=5$

$\Rightarrow x+y-5=0$

 

Q13. Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.

A.13. Let a and b be the intercepts on x and y-axis

Then a + b = 9

$\Rightarrow b=9-a\left(1\right)$

Using intercept form equation of line with a and b intercepts are

$\frac{x}{a}+\frac{y}{b}=1$

$\Rightarrow \frac{x}{a}+\frac{y}{9-a}=1\left(2\right)$

As point (2, 2) passes the line having equation of form equation (2) we can write as

$\frac{2}{a}+\frac{2}{9-a}=1$

$\Rightarrow \frac{2\left(9-a\right)+2a}{a\left(9-a\right)}=1$

$\Rightarrow 18-2a+2a=\left(9-a\right)a$

$\Rightarrow 18=9a-a^2$

$\Rightarrow a^2-9a+18=0$

$\Rightarrow a^2-3a-6a+18=0$

$\Rightarrow a\left(a-3\right)-6\left(a-3\right)=0$

$\Rightarrow \left(a-3\right)\left(a-6\right)=0$

So, a = 3, 6

Case I

When a = 3, b = 9 – 3 = 6. Then the equation of line is

$\frac{x}{3}+\frac{y}{c}=1$

$\Rightarrow \frac{2x+y}{6}=1$

$\Rightarrow 2x+y=6$

$\Rightarrow 2x+y-6=0$

Case II

When a = 6, b = 9 – 6 = 3. Then equation of line is

$\frac{x}{6}+\frac{y}{3}=1$

$\Rightarrow \frac{x+2y}{6}=1$

$\Rightarrow x+2y=6$

$\Rightarrow x+2y-6=0$

Hence, equation of line is 2x + y – 6 or x + 2y – 6 = 0

$\Rightarrow -\surd 3x=y+2\Rightarrow \surd 3x+y+2=0$

 

Q15. The perpendicular from the origin to a line meets it at the point (–2, 9), find the equation of the line.

A.15. The slope of line passing through (0, 0) and (–2, 9) is

$m_1=\frac{y_2-y_1}{x_2-x_1}=\frac{9-0}{-2-0}=\frac{9}{-2}$

The line perpendicular to the line having slope m1 will have the slope

$m_2=\frac{-1}{m_1}=\frac{-1}{-9/2}=\frac{2}{9}$

So, the equation of line with slope m2 and passing  $\left(x_0,y_0\right)=\left(-2,9\right)$ is

$m_2=\frac{y-y_0}{x-x_0}$

$\Rightarrow \frac{2}{9}=\frac{y-9}{x-\left(-2\right)}=\frac{y-9}{x+2}$

$\Rightarrow 2\left(x+2\right)=9\left(y-9\right)$

$\Rightarrow 2x+4=9y-81$

$\Rightarrow 2x-9y+4+81=0$

$\Rightarrow 2x-9y+85=0$

 

Q16. The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110, express L in terms of C.

A.16. Assuming L along y-axis and C along x-axis, we have two points (124.942, 20) and (125.134, 110) in xy-plane. By two-point form, the point L and C satisfies the equation.

y-124.942=  $\frac{(125.134-124.942)}{(110-20)}$ (x-20)

$\Rightarrow$ y-124.942=  $\frac{0.192}{90}$ (x - 20)

$\Rightarrow$ y-124.942=  $\frac{0.032}{15}$ (x - 20)

$\Rightarrow$ 15y – 1874.13=0.032x -0.64

$\Rightarrow$ 15y= 0.032x +1873.49

$\Rightarrow$ y = 0.0021x+124.8993

$\Rightarrow$ L = 0.0021C + 124.8993

 

Q17. The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?

A.17. Assuming the price per litre say P in x-axis and the corresponding demand say D in y-axis, we have two point (14, 980) and (16, 1220) in xy plane. Then the points (P, D) will satisfy the equation.

 

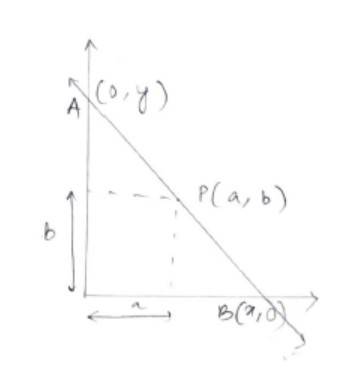
Q18. P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is  $\frac{x}{a}+\frac{y}{b}=2$ .

A.18. Since P(a, b) is the mid-point of the line segment say AB with points A(0, y) and B(x, 0) we can write,

$\left(a,b\right)=\left(\frac{x+0}{2},\frac{y+0}{2}\right)$

$\Rightarrow a=\frac{x}{2}\text{}b=\frac{y}{2}$

$\Rightarrow x=2a\text{}y=2b$

So, the equation of line with x and y intercept 2a and 2b using intercept form is

$\frac{x}{\mathrm{2a}}+\frac{y}{\mathrm{2b}}=1$

$\Rightarrow \frac{x}{a}+\frac{y}{b}=2$

Hence, proved

 

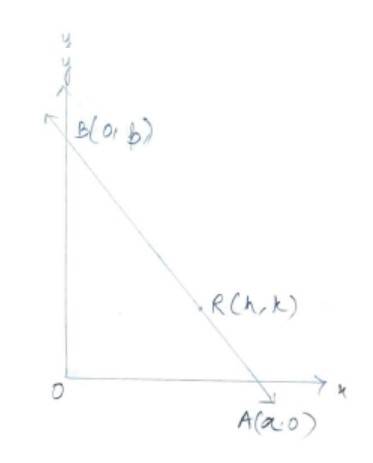
Q19. Point R (h, k) divides a line segment between the axes in the ratio 1: 2. Find equation of the line.

A.19. Equation of line with intercept form is

$\frac{x}{a}+\frac{y}{b}=1\left(1\right)$

As R(h, x) divides line segment joining point A(a, 0) and B(0, b) in the ratio 1 : 2 we can write,

$\left(h,k\right)=\left(\frac{1\times 0+2\times a}{1+2},\frac{1\times b+2\times 0}{1+2}\right)$

So,  $h=\frac{0+2a}{3}k=\frac{b+0}{3}$

$\Rightarrow \mathrm{3h}=2ab=3k$

$\Rightarrow a=\frac{3h}{2}b=3k$

Hence, putting value of aandb in equation (1) we get,

$\frac{x}{3h/2}+\frac{y}{\mathrm{3k}}=1$

$\Rightarrow \frac{x}{\mathrm{3h}}+\frac{y}{\mathrm{3k}}=1$

 

Q20. By using the concept of equation of a line, prove that the three points (3, 0), (– 2, – 2) and (8, 2) are collinear.

A.20. Let the given points be A(3, 0), B(–2, –2) and C(8, 2). Then by two point form we can write equation of line passing point A(3, 0) and B(–2, –2) as

$y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)$

$\Rightarrow y-0=\frac{-2-0}{-2-3}\left(x-3\right)$

$\Rightarrow y=\frac{-2}{-5}\left(x-3\right)$

$\Rightarrow 5y=2\left(x-3\right)$

$\Rightarrow 5y=2x-6$

$\Rightarrow 2x-5y-6=0\left(1\right)$

If the three points A, B and C are co-linear, C will also lieonm the line formed by AB or satisfies equation (1).

Hence, putting x = 8 and y = 2 we have

L.H.S. = 2 × 8 – 5 × 2 – 6

= 16 – 10 – 6

= 0 = R.H.S.

The given three points are collinear.

 

Exercise 10.3

Q1. Reduce the following equations into slope - intercept form and find their slopes and the y - intercepts.

(i) x + 7y = 0, (ii) 6x + 3y – 5 = 0, (iii) y = 0.

A.1. (i) Given, x + 7y = 0.

7y = -x

y =  $\frac{-1}{7}$ x + 0.

Comparing the above equation with y = mx + c we get, slope, m = - $\frac{1}{7}$ and c = 0, y-intercept

(ii) Given, 6x + 3y - 5 = 0

3y = -6x + 5

y = - $\frac{6}{3}$ x +  $\frac{5}{3}$ = -2x +  $\frac{5}{3}$

Comparing the above equation with y = mx + c we get, slope, m = -2 and $c=\frac{5}{3}$ , y-intercept

(iii) Given, y = 0

y = 0xx + 0

Comparing the above equation with y = mx + c we get, Slope, m = 0 and c = 0,y-intercept.

 

Q2. Reduce the following equations into intercept form and find their intercepts onthe axes.

(i) 3x + 2y – 12 = 0, (ii) 4x – 3y = 6, (iii) 3y + 2 = 0.

A.2. (i) Given, 3x + 2y 12 = 0.

3x + 2y = 12

Dividing both sides by 12 we get,

$\Rightarrow \frac{3x}{12}+\frac{2y}{12}=\frac{12}{12}$

$\Rightarrow \frac{x}{4}+\frac{y}{6}=1.$

Comparing the above equation with  $\frac{x}{a}+\frac{y}{b}=1$ = we get, x-intercept, a = 4 and y-intercept b = 6.

(ii) Given, 4x - 3y = 6

Dividing the both sides by 6.

$\frac{4x}{6}-\frac{3y}{6}=\frac{6}{6}$

$\Rightarrow \frac{2x}{3}-\frac{y}{2}=1$

$\Rightarrow \frac{x}{3/2}+\frac{y}{(-2)}=1.$

Comparing above equation by  $\frac{x}{a}+\frac{y}{b}=1$ we get, x-intercept a =  $\frac{3}{2}$ and y-intercept, b = -2

(iii) Given, 3y + 2 = 0.

3y = -2

$y=-\frac{2}{3}$

As the equation of line is of form y = constant, it is parallel to x-axis and has no x-intercept.

Qy-intercept = - $\frac{2}{3}$

As w lies in IVth quadrant

Cos w = cos 45 ° and sin w = sin 45°

= cos (360° -  45°)= sin (360° -  45°)

= cos 315°= sin 315°

So, w = 315°

 

Q4. Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).

A.4. The given equation of the line is.

12(x + 6) = 5 (y - 2)

12x + 72 = 5y - 10

12x - 5y + 72 + 10 = 0

12x - 5y + 82 = 0

4x - 12 = 20

x  $=\frac{20+12}{4}=\frac{32}{4}=8$

Case II.  $\frac{4x-12}{-5}=4$

4x - 12 = 20

x =  $\frac{-20+12}{4}=\frac{-8}{4}=-2$

x = -2

So, the points on x-axis one (8, 0) and (-2, 0)

 

Q7. Find equation of the line parallel to the line 3x − 4y + 2 = 0 and passing throughthe point (–2, 3).

A.7. The slope of the line 3x - 4y + 2 = 0 is,

$m=-\frac{}{}<math>\; <mrow>\; <mfrac>\; <mrow>\; <mn>\; 3\; </mn>\; </mrow>\; <mrow>\; <mn>\; 4\; </mn>\; </mrow>\; </mfrac>\; </mrow>\; </math>\; <br>=\; -\frac{3}{-4}=\frac{3}{4}$

So, slope of line parallel to 3x - 4y + 2 = 0 is also m= $\frac{3}{4}$ .

Hence, this parallel line passes through ( -2, 3) we can write,

$m=\frac{y-y_0}{x-x_0}$

$\frac{3}{4}=\frac{y-3}{x-(-2)}=\frac{y-3}{x+2}$

3(x + 2) = 4(y - 3)

3x + 6 = 4y - 12

3x - 4y + 6 + 12 = 0.

3x - 4y + 18 = 0. Which is the required equation of line.

 

Q13. Find the equation of the right bisector of the line segment joining the points (3, 4)and (–1, 2).

A.13. Let P(3, 9) and Q (-1, 2) be the point. Let M bisects PQ at M so,

Co-ordinate of M =  $\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$

$=\left(\frac{3+(-1)}{2},\frac{4+2}{2}\right)$

$=\left(\frac{3-1}{2},\frac{6}{2}\right)=\left(\frac{2}{2},\frac{6}{2}\right)=(1,3)$

Now, slope of AB, m =  $\frac{y_2-y_1}{x_2-x_1}=\frac{2-4}{-1-3}=\frac{-2}{-4}=\frac{1}{2}.$

As the bisects AB perpendicular it has slope  $-\frac{1}{m}$ and it passes through M(1, 3) it has the equation of the form,

$\frac{-1}{m}=\frac{y-y{}_{\mathrm{\sigma }}}{x-x{}_0}$

$\frac{-1}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=\frac{y-3}{x-1}$

$\Rightarrow -2=\frac{y-3}{x-1}$

$\Rightarrow -2(x-1)=y-3$

$\Rightarrow -2x+2=y-3$

$\Rightarrow 2x+y-3-2=0$

2x + y - 5 = 0

 

Q14. Find the coordinates of the foot of perpendicular from the point (–1, 3) to theline 3x – 4y – 16 = 0.

 

A.14. Let P(-1, 3) be the given point and Q(x, y,) be the Co-ordinate of the foot of perpendicular

So, slope of line 3x - 4y - 16 = 0 is

$m_1=\frac{-3}{-4}=\frac{3}{4}$

And slope of line segment joining P(-1, 3) and Q(x, y,) is

$m_2=\frac{y_1-3}{x_1-(-1)}=\frac{y_1-3}{x_1+1}$

As they are perpendicular we can write as,

$m_1=\frac{-1}{m_2}$

$\frac{3}{4}=-\frac{1}{\left(y_1-{3/x}_{}+1\right)}$

$\Rightarrow \frac{3}{4}=-\frac{\left(x_1+1\right)}{\left(y_1-3\right)}$

(y₁-3)3 = - 4(x₁ +1)

3y₁- 9 = - 4x₁- 4.

4x₁ + 3y₁-9 + 4 = 0

4x₁ + 3y₁-5 = 0 ___ (1)

As point Q(x₁, y₁) lies on the line 3x- 4y - 16 = 0 it must satisfy the equation hence,

3x₁- 4y₁- 16 = 0 ____ (2)

Now, multiplying equation (1) by 4 and equation (2) by 3 and adding then,

4× (4x₁ + 3y₁- 5) + 3(3x₁- 4y₁- 16) = 0.

16x₁ + 12y₁- 20 + 9x₁- 12y₁- 48 = 0

25x₁ = 48 + 20

$\Rightarrow x_1=\frac{68}{25}$ .

Putting value of x₁ in equation (1) we get,

$4\times \frac{68}{25}+3y_1-5=0$

4× 68 + 25× 3y₁ = 25 ×5.

25× 3y₁ = 125 - 272

$y_1=\frac{-147}{25\times 3}$

$\Rightarrow y_1=-\frac{49}{25}$

 

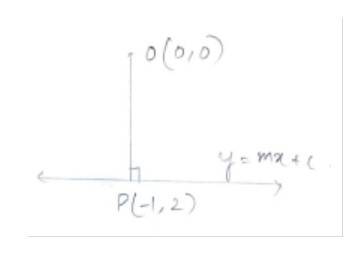
Q15. The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the values of m and c.

A.15. Let 0(o, o) be the origin and P(-1, 2) be the given point on the line y = mx + c.

Then, slope of OP, =  $=\frac{2-0}{-1-0}$

Slope of OP = -2

As the line y = mx + c is ⊥ to OP we can write

 

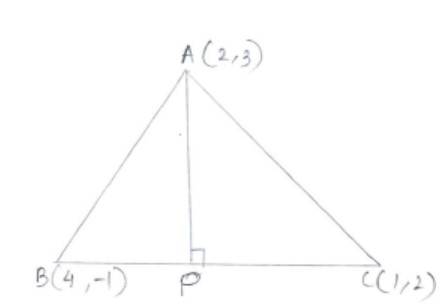
Q17. In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.

A.17. Let P be the point on the BC dropped from vertex A.

Slope of BC $=\frac{\mathrm{2\; -}<br>\mathrm{(-1)}}{1\; -4}$

$=\frac{2+1}{-3}$

$=\frac{3}{-3}$

=  $-$ 1.

As A P  $\perp$ BC,

Slope of AP=  $\frac{-1}{\mathrm{slope\; of\; B}C}=\frac{-1}{-1}=1.$  $$

Using slope-point form the equation of AP is,

$1=\frac{y-3}{x-2}$

$\Rightarrow$ x  $-$ 2 = y  $-$ 3

$\Rightarrow$ x – y – 2 + 3 = 0  $\Rightarrow$ x – y + 1 = 0

The equation of line segment through B(4, -1) and C(1, 2) is.

$y-(-1)=\frac{2-(-1)}{1-4}(x-4).$

$\Rightarrow y+1=\frac{2+1}{-3}(x-4)$

$\Rightarrow (y+1)=\frac{3}{-3}(x-4).$

$\Rightarrow y+1=-(x-4)$

$\Rightarrow xy+1=-x+4$

$\Rightarrow -x+y+1-4=0$

$\Rightarrow$  $x+y-3=0$

So, A=1, B=1 and C=  $-$ 3.

Hence, length of AP=length of  $\perp$ distance of A(2,3) from BC.

Q18. If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that  $\frac{1}{p^2}=\frac{1}{b^2}+\frac{1}{a^2}.$

A.18.The equation of line whose intercept on axes are a and b is given by,

$\frac{x}{a}+\frac{y}{b}=1.$

Multiplying both sides by ab we get,

$\frac{abx}{a}+\frac{aby}{b}=ab$

$\Rightarrow bx+ay-ab=0.$

 

Miscellaneous

Q1.Find the values of k for which the line (k–3) x – (4 – k2) y + k2 –7k + 6 = 0 is

(a) Parallel to the x-axis,

(b) Parallel to the y-axis,

(c) Passing through the origin.

A.1. We have, (k - 3) x - (4 - k²) y + k² - 7 y + 6 = 0.

(i) When the line is parall to x-axis, all x coefficient = 0. then,

(k - 3)x - (4 -k²)y + k² - 7y + 6 = 0 x.x - a x y       where a = constant

Equating the co-efficient,

K – 3 = 0

=> k = 3

(ii) When the line is parallel to y-axis all y co-efficient = 0 then

- (4 -k)² = 0

=> – 4 + x² = 0

k² = 4

k = ± 2.

(iii) When the line pares through origin, (0, 0) need satisfy the given eqn then,

k² - 7k + 6 = 0

k² - k – 6k + 6 = 0

k (k- 1) - 6 (k - 1) = 0

(k = 1) (k - 6) = 0

k = 1 and k = 6

 

Q2. Find the values of q and p, if the equation x cosØ  + y sinØ = p is the normal form of the line √3 $x+y+2=0.$

A.2. The given equation of the line is  $$ √3x + y + 2 = 0

 

Q3. Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and – 6, respectively.

A.3. Let a and b be the x & y intercept. Then,

$\frac{x}{a}+\frac{y}{b}=1.$ _____ (1)

Given, a + b = 1. ______ (2) b = 1 – a _____ (3)

and ab = –6 _____ (4)

Putting eqn (B) in (iii) we get a

a(1- a) = - 6

a - a² = - 6

a² - a - 6 = 0

a² + 2a - 3a - 6 = 0

a (a + 2) - 3 (a + 2) = 0

(a + 2) (a – 3) = 0

(a + 2) (a – 3) = 0.

a = 3 or a = – 2.

When a = 3, b = 1– a = 1 – 3 = – 2

When a = – 2, b = 1 – (–2) = 1 + 2 = 3

So, (a, b) = (3, – 2) and (– 2, 3)

Hence, eqⁿ(1) becomes,

$\frac{x}{3}+\frac{y}{-2}=1$ and  $\frac{x}{-2}+\frac{y}{3}=1.$

2x – 3y = 6 and 2y – 3x = 6

Gives the read eqⁿ of lines

 

Q4. What are the points on the y-axis whose distance from the line  $\frac{x}{3}+\frac{y}{4}=1$ is 4 units.

A.4. Let (0, y) be the point on y-axis which is at a distance 4 unit from the line  $\frac{x}{3}+\frac{y}{4}=1$

 

Q6. Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.

A.6. The given eqn of lines are

x – 7y + 5 = 0 ______ (1) x = 7y – 5

and 3x + y = 0 _________ (2)

Solution (1) and (2) we get,

3 [7y – 5] + y = 0 .

21y – 15 + y = 0

=> 22y = 15

y =  $\frac{15}{22}$

So, x =  $7\times \frac{15}{22}-5=\frac{105-110}{22}=-\frac{5}{22}.$

The point of intersection of line (1) and (2) is

$\left(\frac{-5}{22}·\frac{15}{22}\right)$

Eqⁿ of line through $\left(\frac{-5}{22},\frac{15}{22}\right)$ and parallel to y - axis is,  $x=-\frac{5}{22}.$

 

Q7. Find the equation of a line drawn perpendicular to the line $\frac{x}{3}+\frac{y}{6}=1$ through the point, where it meets the y-axis.

A.7. The given Eqⁿ of the line is $\frac{x}{4}+\frac{y}{6}$ = 1 ______ (1)

so, Slope of line = - $\frac{6}{4}=-\frac{3}{2}.$

The line ⊥ to line (1) say l₂ has

Slope of l₂ = $\frac{-1}{(-3/2)}=\frac{2}{3}.$

Let P (0, y) be the point of on y-axis where it is cut by the line (1)

Then,  $\frac{0}{4}+\frac{y}{6}=1$

y = 6

i.e, the point P has co-ordinate (0, 6)

ø Eqⁿ of line ⊥ to $\frac{x}{4}+\frac{y}{6}=1$ and cuts y-axis at P (0,6) is

y – 6 = $\frac{2}{3}$ (x – 0)

3y – 18 = 2x

2x – 3y + 18 = 0

 

Q8. Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.

A.8. The given eqⁿ of the lines are

y – x = 0 _____ (1)

x + y = 0 ______ (2)

x – k = 0 ______ (3)

The point of intersection of (1) and (2) is given by

(y – x) – (x + y) = 0

y – x – x – y = 0

y = 0 and x = 0

ie, (0, 0)

The point of intersection of (2) and (3) is given by

(x + y) – (x – k) = 0

y + k = 0

y = –k and x = k

i.e, (k, –k)

The point of intersection of (3) and (1) is given by

x = k

and y = k

ie, (k, k).

Hence area of triangle whose vertex are (0, 0), (k, –k)

and (k, k) is

area (A) =  $\frac{1}{2}|$ x1 (y2 – y3) + x3 (y3 – y1) + x2 (y1 – y2) $\begin{array}{l}\\ \end{array}|$

=  $\frac{1}{2}|$ 0 ( –k – k) + k (k – 0) + k (0 – (–k)) $\begin{array}{l}\\ \end{array}|$

$\frac{1}{2}|$k2 + k2 $\begin{array}{l}\end{array}|$ = k2 unit2

 

Q9. Find the value of p so that the three lines 3x + y – 2 = 0, px + 2 y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.

A.9. The given eqⁿ of the lines are.

3x + y – 2 = 0 _____ (1)

Px + 2y – 3 = 0 ______ (2)

2x – y – 3 = 0 _____ (3)

Point of intersection of (1) and (3) is given by,

(3x + y – 2) + (2x – y – 3) = 0

=> 5x – 5 = 0

=> x =  $\frac{5}{5}$

=> x = 1

So, y = 2 – 3x = 2 – 3 (1) = 2 – 3 = 1.

i e, (x, y) = (1, –1).

As the three lines interests at a single point, (1, –1) should line on line (2)

i e, P × 1 + 2 × (–1)– 3 = 0

P – 2 – 3 = 0

P = 5

 

Q10. If three lines whose equations are y = m₁x + c₁, y = m₂x + c₂ and y = m₃x + c₃ are concurrent, then show that m₁(c₂ – c₃) + m₂ (c₃ – c₁) + m₃ (c₁ – c₂) = 0.

A.10. The given eqⁿ of the three lines are

y = m₁ x + c₁ ______ (1)

y = m₂ x + c₂ ______ (2)

y = m₃ x + c₃ ______ (3)

The point of intersection of (2) and (3) is given by.

y – y = (m₂x + c₂) - (m₃ x + c₃)

(m₂ - m₃) x = c₃ - c₂

$\Rightarrow x=\frac{c_3-c_2}{m_2-m_3}.$

Hence, y =  $\frac{m_2\left(c_3-c_2\right)}{\left(m_2-m_3\right)}+c_2$

$=\frac{m_2\left(c_3-c_2\right)+c_2\left(m_2-m_3\right)}{m_2-m_3.}$

$=\frac{m_2{c}_3-m_3{c}_2}{m_2-m_3}.$

$ie,\left(\frac{c_3-c_2}{m_2-m_3},\frac{m_2{c}_3-m_3{c}_2}{m_2-m_3}\right)$

As the three lines are concurrent, the point of intersection of (2) and (3) lies on line (1) also

i e,  $\frac{m_2{c}_3-m_3{c}_2}{m_2-m_3}=m_1\left(\frac{c_3-c_2}{m_2-m_3}\right)+c_1$

$\Rightarrow \frac{-m_1\left(c_2-c_3\right)+c_1\left(m_2-m_3\right)}{m_2-m_3}=\frac{-m_2{c}_3-m_3{c}_2}{m_2-m_3}.$

m₁ (c₂ - c₃) - c₁ (m₂ - m₃) + m₂ c₃ - m₃ c₂ = 0

m₁ (c₂ - c₃) - m₂ c₁ + m₃ c₁ + m₂ c₃ - m₃ c₂ = 0

m₁ (c₂ - c₃) + m₂ (c₃ - c₁) + m₃ (c₁ - c₂) = 0

 

Q11. Find the equation of the lines through the point (3, 2) which make an angle of 45^o with the line x – 2y = 3.

A11. x – 2y = 3

y = $\frac{\mathrm{x}}{2}$ - $\frac{3}{2}$______ (1)

Slope of line (1) is  $\frac{1}{2}\cdot$

Let the line through P(3, 2) have slope m

Then, angle between the line =  $\left|\frac{m-\frac{1}{2}}{1+m\frac{1}{2}}\right|$

$\Rightarrow tan45^{°}=\left|\frac{2m-1}{2+m}\right|$

$\Rightarrow 1=\left|\frac{2m-1}{2+m}\right|$

$\Rightarrow \frac{2m-1}{2+m}=\pm 1.$

When,  $\frac{2m-1}{2+m}=1$ =>2m – 1 = 2 + m=> m = 3.

The eqn of line through (3, 2) is

y – 2 = 3 (x – 3) 3x – y – 7 = 0.

When  $\frac{2m-1}{2+m}$ = – 1=> 2m – 1 = – 2 – m =>3m = – 1 m = $-\frac{1}{3}$

The equation of line through (3,2) is,

y – 2 =  $-\frac{1}{3}$ (x – 3) => 3y – 6 = – X + 3

x + 3y – 9 = 0

 

Q12. Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.

A.12. The given eqn of the line is.

4x + 7y – 3 = 0 _____ (1)

2x – 3y + 1 = 0 _______ (2)

Solving (1) and (2) using eqn (1) 2 x eqn (2) we get,

(4x + 7y – 3) 2 [(2x – 3y + 1)] = 0

4x + 7y – 3 – 4x + 6y – 2 = 0

13y = 5

y =  $\frac{5}{13}$

And 2x – 3  $\left(\frac{5}{13}\right)$ + 1 = 0

2x =  $\frac{15}{13}$ – 1 =  $\frac{2}{13}$

$\Rightarrow x=\frac{1}{13}$

Point of intersection of (1) and (2) is  $\left(\frac{1}{13},\frac{5}{13}\right)$

Since, the line passing through  $\left(\frac{1}{13},\frac{5}{13}\right)$ has equal intercept say c then it is of the form

$\frac{x}{c}+\frac{y}{c}=1.$

x + y = c

$\Rightarrow \frac{1}{13}+\frac{5}{13}=c$

c =  $\frac{6}{13}$

the read eqn of line is x + y =  $\frac{6}{13}$

13x + 13y – 6 = 0

 

Q13. Show that the equation of the line passing through the origin and making an angle ø with the line $y=mx+cis\frac{y}{x}=\frac{m\pm tan,}{m\mp tan,}.$

A.13. The given eqⁿ of line is.

l₁ : y = mx + c.

Slope of l₁ = m

Let m՛ be the slope of line passing through origin (0, 0) and making angle Ø with l₁

Thus, (y 0) = m՛ (x 0)

y = m՛ x

m՛ =  $\frac{\mathrm{y}}{\mathrm{<br>}\mathrm{x}}$______ (1)

And tanØ =  $\left|\frac{m^{\prime }-m}{1+m^{\prime }·m}\right|$ =  $\frac{m^{\prime }-m}{1+m^{\prime }m}$

When, tanØ =  $\frac{m^{\prime }-m}{1+m^{\prime }m}.$

tanØ + m՛ m tanØ = m’ - m

m + tanØ = m՛ - m՛m tanØ

m' = $\frac{m+tan\theta }{1-mtan\theta }.$

When tan Ø =  $-\left(\frac{m^{\prime }-m}{1+m^{\prime }m}\right)$

tan θ + m՛ m tanØ = -m՛ + m

m' = $\frac{m-tan\theta }{1+mtan\theta }.$

Hence combining the two we get,

$m^{\prime }=\frac{m\pm tan\theta }{1\mp mtan\theta }.$

$\Rightarrow \frac{y}{x}=\frac{m\pm tan\theta }{1\mp mtan\theta }.$ {-: eqⁿ (1) }

 

Q14. In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?

A.14. The given eqⁿ of line is

l1: x + y = 4

Let R divides the line joining two points P(‒1,1) and Q(5,7) in ratio k:1. Then,

Co-ordinate of R = ( $\left(\frac{5k-1}{k+1},\frac{7k+1}{k+1}\right)$)

As l₁ divides line joining PQ, then R lies on l₁

i e,  $\left(\frac{5k-1}{k+1},\frac{7k+1}{k+1}\right)$=4

5k ‒1 + 7k + 1= 4(k + 1)

12k = 4k + 4

8k = 4

k =  $\frac{1}{2}$

The ratio in which x + y = 4 divides line joining (‒1,1) ad (5,7) is  $\frac{1}{2}$ :1 i.e., 1: 2.

 

Q15. Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.

A.15. The given eqⁿ of the lines are.

4x + 7y + 5 = 0______ (1)

2x – y = 0 ______ (2)

Solving (1) and (2) we get,

4 x + 7(2 x)+5 = 0

4x +14 x + 5= 0

x =  $\frac{-5}{18}$

and y = 2x =  $2\left(\frac{-5}{18}\right)=\frac{-5}{9}$

 

Q24. A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.

A.24. If point P be the junction between the lines

2x – 3y + 4 = 0 ______ (1)

3x + 4y – 5 = 0 ______ (2)

Solving (1) and (2) using 3 × (1) – 2 × (2) we get,

6x – 9y + 12 – (6x + 8y – 10) = 0

–17y + 22 = 0

y =  $\frac{22}{17}$

And 2x = 3y– 4

=> 2x = 3 × $\frac{22}{17}$ – 4

x =  $\frac{33}{17}$ – 2 =  $\frac{33-34}{17}$ =  $-\frac{1}{17}$

Hence, the co-ordinate of the junction is P  $\left(-\frac{1}{17},\frac{22}{17}\right)$

The eqⁿ of the path to be reach is

6x – 7y + 8 = 0 _____ (3)

Then, least distance will be perpendicular path.

So, slope of ⊥ path = $-\frac{1}{\mathrm{<br>}\mathrm{slope\; of \; line\; (3)}}$ $\begin{array}{c}<br>\\ \end{array}$

$=\frac{-1}{(6/7)}=\frac{-7}{6}$

Hence eqⁿ of shortest/least distance path from P $\left(-\frac{1}{17},\frac{22}{17}\right)$is

$y-\frac{22}{17}=\frac{-7}{6}\left(x+\frac{1}{17}\right).$

$\Rightarrow 6y-\frac{132}{17}=-7x-\frac{7}{17}.$

$\Rightarrow 7x+6y-\frac{132}{17}+\frac{7}{17}=0$

$\Rightarrow 7x+6y-\frac{125}{17}=0.$

119x + 102y – 125 = 0