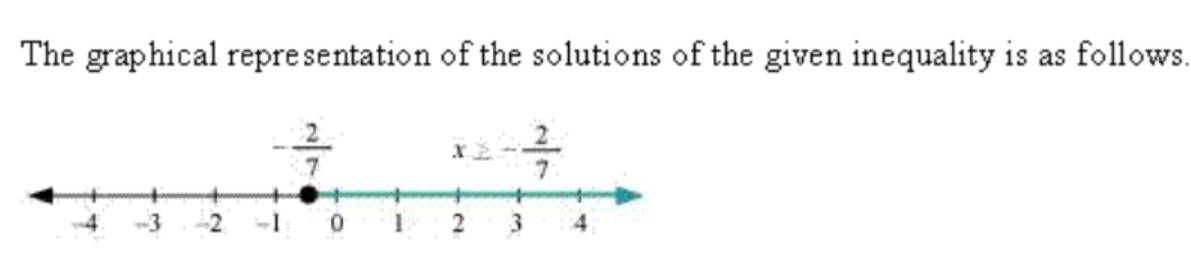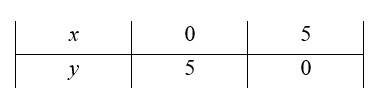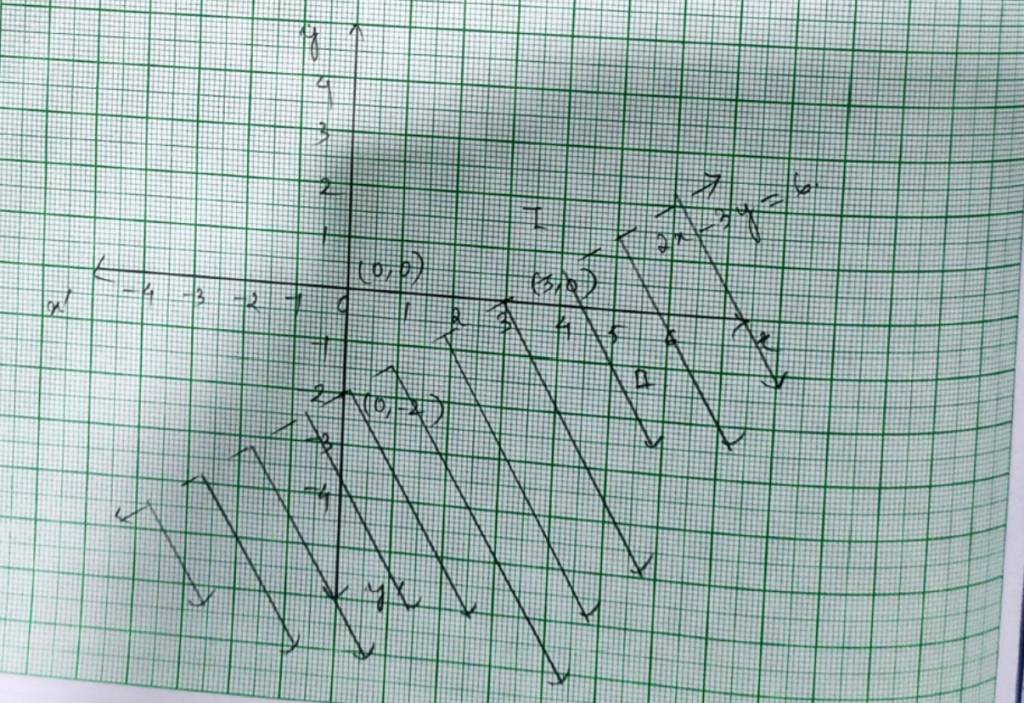NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities: Overview, Questions, Preparation

Ex 6.1

Q1. Solve 24x < 100, when

(i) x is a natural number. (ii) x is an integer.

A.1. 24x < 100.

Dividing both sides by 24 we get,

$\frac{24x}{24}<\frac{150}{24.}$

x<  $\frac{25}{6}$ = 4.166

(i) As x is a natural no the solⁿ of the given inequality are 1, 2, 3, 4.

(ii) As x is an integer the solⁿ of the given inequality are 4, 3, 2, 1, 0, 1, 2, 3, ….

 

Q2. Solve – 12x > 30, when

(i) x is a natural number. (ii) x is an integer.

A.2. – 12 x> 30.

Dividing both sides by 12 we get,

$-x>\frac{30}{12}$

$-x>\frac{5}{2}$

Multiplying both side by ( – 1) the inequality will change.

i e, x<  $\frac{5}{2}$ = – 2.5

(i) As x is a natural number, the soln of the given inequality does not exist in natural numbers.

(ii) As x is an integer, the soln of the given inequality will be all the integer less than – 5/2

i. e, – 3, – 4, – 5, …..

 

Q3. Solve 5x – 3 < 7, when

(i) x is an integer. (ii) x is a real number.

A.3. Given, 5x – 3 < 7.

5x – 3 + 3 < 7 + 3

5x< 10

$\frac{5x}{5}<\frac{10}{5}$

x< 2.

when x∈z, i. e, x is an integer all integers less than 2 are the solⁿ so, x = {…., – 3, – 2, – 1, 0, 1}

(ii) when x ∈ R i, e x is a real number all t real number less than 2. are the soln.

So, x∈ (– , 2)

 

Q4. Solve 3x + 8 >2, when

(i) x is an integer. (ii) x is a real number.

A.4. Given, 3x + 8 > 2

3x + 8 – 8 > 2 – 8

3x> – 6

$\Rightarrow \frac{3x}{3}>-\frac{6}{3}$

x> – 2

(i) when x is an integer, x ∈z all integer greater than – 2 are the soln. so, x = { – 1, 0, 1, 2, 3, …}.

(ii) when x is a real number, all real number greater than – 2 are the soln. so, x ( –2,∞  )

Solve the inequalities in Exercises 5 to 16 for real x.

 

Q5. 4x + 3 < 5x + 7

A.5. Given,

4 x+ 3 < 5 x+7.

3–7<5 x –4 x.

–4

So, x ( –4,∞)

 

Q6. 3x – 7 > 5x – 1

A.6. Given, 3x–7 > 5x–1.

7+1> 5x–3x

6> 2x

$\Rightarrow \frac{-6}{2}>\frac{2x}{2}$

–3 > x

So, x ∈(–∞,– 3)

 

Q7. 3(x – 1) ≤ 2 (x – 3)

A.7. 3(x –1) ≤ 2(x –3)

3x– 3 ≤ 2x –6

=> 3x– 2x ≤ –6 + 3

x ≤ –3

So, x ∈(–∞,– 3]

 

Q8. (2 – x) ≥2 (1 – x)

A.8. 3(2 – x) ≥2(1 – x)

6 – 3x ≥ 2 – 2x

6– 2≥ 3x– 2x

4≥ x

So, x∈ (–∞, 4]

 

Q9.  $x+\frac{x}{2}+\frac{x}{3}<11$

A.9. x + $\frac{x}{2}+\frac{x}{3}$ < 11

$\Rightarrow \frac{6x+3x+2x}{6}<11$

$\Rightarrow \frac{(6x+3x+2x)\times 6}{6}<11\times 6$

11x< 66

$\frac{11x}{11}<\frac{66}{11}$

x< 6.

So, x∈ (–∞, 6)

 

Q10. $\frac{x}{3}>\frac{x}{2}+1$

A.10. Given, $\frac{x}{3}>\frac{x}{2}+1$

$\Rightarrow \frac{x}{3}-\frac{x}{2}>1$

$\Rightarrow \frac{2x-3x}{6}>1$

$\Rightarrow \frac{(2x-3x)\times 6}{6}>1\times 6$

x> 6

x< –6.

So, x (–∞, –6)

 

Q11.  $\frac{3\left(x-2\right)5}{5}\le \frac{5\left(2-x\right)}{3}$

A.11. Given, $\frac{3\left(x-2\right)5}{5}\le \frac{5\left(2-x\right)}{3}$

=> 3 x 3(x – 2) ≤ 5 x 5(2 – x)

=> 9x – 18 ≤ 50 – 25x

=> 9x + 25x ≤ 50 + 18

=> 34x ≤ 68

=>  $x=\frac{68}{34}$

=> x ≤ 2

So,  $$  $x\in (-\infty ,2]$

 

Q12.  $\frac{1}{2}\left(\frac{3x}{5}+4\right)\ge \frac{1}{3}\left(x-6\right)$

A.12. Given, $\frac{1}{2}$  $\left(\frac{3x}{5}+4\right)\ge \frac{1}{3}(x-6)$

$\frac{6}{2}\left(\frac{3x}{5}+4\right)\ge \frac{6}{3}(x-6)$

$\Rightarrow 3\left(\frac{3x}{5}+4\right)\ge 2(x-6)$

$\Rightarrow \frac{9}{5}x+12\ge 2x-12$

$\Rightarrow \frac{9}{5}x-2x\ge -12-12.$

$\Rightarrow \frac{9x-10x}{5}\ge -24.$

$\Rightarrow \frac{-x\times 5\ge }{5}-24\times 5.$

x ≥–120.

(–1) x (–x)≤ ( –120)× (–1)

x ≤ 120.

So, x ∈(–∞, 120].

 

Q13. 2 (2x + 3) – 10 < 6 (x – 2)

A.13. Given 2 (2x + 3) –10 < 6 (x –2)

4x + 6 –10 < 6x– 12.

4x –4 < 6x –12

12 –4 < 6x –4x

8 < 2x

$\Rightarrow \frac{8}{2}<\frac{2x}{2}\Rightarrow 4<x$

So, x∈ (4, –∞)

 

Q14. 37 – (3x + 5) ≥ 9x – 8 (x – 3)

A.14. Given, 37 –(3x + 5) ≥9x –8 (x –3)

37– 3x–5 ≥9x –8x+ 24.

37 – 24–5 ≥9x –8x+ 3x

8 ≥4x.

$\Rightarrow \frac{8}{4}\ge x$

2 ≥x

So, x∈ (–∞, 2]

 

Q15.  $\frac{x}{4}<\frac{\left(5x-2\right)}{3}-\frac{\left(7x-3\right)}{5}$

A.15. Given, $\frac{x}{4}<\left(\frac{5x-2}{3}\right)-\left(\frac{7x-3}{5}\right)$

$\frac{x}{4}<\frac{5\times (5x-2)-3(7x-3)}{3\times 5.}$

15x<4[25x–10–21x+9]

15x< 4 [4x –1]

15x< 16x–4

4 < 16x –15x

4. <. x

So, x ∈(4,∞ )

 

Q16.  $\frac{\left(2x-1\right)}{3}\ge \frac{\left(3x-2\right)}{4}-\frac{\left(2-x\right)}{5}$

A.16. Given,

$\frac{2x-1}{3}\ge \frac{3x-2}{4}-\frac{2-x}{5}$

$\frac{(2x-1)}{3}\ge \frac{5(3x-2)-4(2-x)}{4\times 5}$

20(2x- 1) ≥3 [15x- 10 - 8 + 4x].

40x-20 ≥3[19x-18]

40x-20 ≥ 57x – 54.

54 - 20 ≥ 57x- 40x

34 ≥17x

$\Rightarrow \frac{34}{17}\ge x.$

2 ≥x

So, x(- ∞, 2].

Solve the inequalities in Exercises 17 to 20 and show the graph of the solution in each case on number line

 

Q17. 3x – 2 < 2x + 1

A.17. Given, 3x – 2 < 2x + 1

3x – 2x< 2 + 1

x< 3.

So, x (- ∞,, 3).

 

 

Q18. 5x – 3 > 3x – 5

A.18. Given, 5x – 3 > 3x 5

5x –3x≥ –5 + 3.

2x ≥ –2.

x  $\frac{-2}{2}$

x ≥ –1.

So, x [1,- ∞ ).

 

 

Q19. 3 (1 – x) < 2 (x + 4)

A.19. Given, 3(1–x) < 2(x + 4)

3 –3x< 2x + 8

3–8< 2x+ 3x

–5 < 5x

$\frac{-5}{5}<x$

1

So, x (–1,∞ )

 

Q20.  $\frac{x}{2}\ge \frac{\left(5x-2\right)}{3}-\frac{\left(7x-3\right)}{5}$

A.20. Given,

$\frac{x}{2}\ge \frac{(5x-2)}{3}-\frac{(7x-3)}{5.}$

$\Rightarrow \frac{x}{2}\ge \frac{5(5x-2)-3(7x-3)}{3\times 15}$

15x ≥2[25x –10 –21x + 9].

15x ≥2[4x –1]

15x≥ 8x –2

15x –8x ≥–2

7x ≥–2

x ≥ $-\frac{2}{7}.$

So, x  $\left[-\frac{2}{7},\infty \right)$  $\left\{\therefore -\frac{2}{7}=-0.28\right\}$

 

 

Q21. Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.

A.21. Let x be the marks obtained by Ravi in third test.

Then, average mark≥ 60

$\Rightarrow \frac{70+75+x}{3}\ge 60$

145 + x≥ 180.

x ≥180 - 145

x≥ 35.

So minimum mark required = 35.

 

Q22. To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.

A.22. Let ‘x’ be the marks obtained by Sunita in the 5th exam.

Then, average marks ≥ 90.

$\frac{87+92+94+95+x}{5}\ge 90$ .

368 + x ≥90 × 5.

368 + x ≥450.

x ≥ 450 - 368.

x.≥ 82.

Minimum mark required= 82.

 

Q23. Find all pairs of consecutive odd positive integers both of which are smaller than10 such that their sum is more than 11.

A.23. Let x be the smaller of the consecutive odd positive integers, then the. other is x + 2 {Since the consecutive odd number are differ by 2.}

then the. other is x + 2

so, x< 10 and x + 2 < 10 x< 8

and x + (x + 2) > 11.

2x> 11 - 2

2x> 9

$\Rightarrow x>\frac{9}{2}$

and hence,  $\frac{9}{2}<x<8.$

4.5

As x∈z, x = 5 and x = 7

and x is odd

The reqd. possible pairsby (x, x + 2) are (5, 7),(7, 9).

 

Q24. Find all pairs of consecutive even positive integers, both of which are larger than5 such that their sum is less than 23.

A.24. Let x be the smaller no. of the two consecutive even positive integers, hence the other number is x + 2.(Two consecutive even no. differs by 2).

Then, x> 5, x + 2 > 5  =>a> 3.

And x +(x + 2) < 23

2x + 2 < 23

2x< 23 - 2

2x< 21

$\Rightarrow x<\frac{21}{2}=10.5.$

So, 5 2 1 2 , x∈z and x is positive.

Hence, x can take the value 6, 8 and 10.

So, the required possible pair is given by (x, x + 2) are (6, 8), (8, 10) and (10, 12).

 

Q25. The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.

A.25. Let x cm be the shortest side of the triangle.

Thus, the other 2 sides are “3x”cm and “3x - 2”. cm

Given, perimeter of A triangle ≥ 61

x + 3x - 3x- 2 ≥61

7x - 21≥ 61

7x ≥ 61 + 21

$\Rightarrow x\ge \frac{82}{7}$

x ≥ 9.

The minimum length of the shortest side is 9 cm.

 

Q26. A man wants to cut three lengths from a single piece of board of length 91cm.The second length is to be 3cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5cm longer than the second?

[Hint: If x is the length of the shortest board, then x , (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x + (x + 3) + 2x ≤ 91 and2x ≥ (x + 3) + 5].

A.26. Let ‘x’ cm be the length of shortest piece.

Then, the two other remaining length is.

(x + 3) cm and (2x). cm.

So, given that,

2x - (x + 3) ≥ 5 cm.

2x- x - 3 ≥ 5.

x ≥ 5 + 3

x ≥ 8.

And. total length ≤ 91 cm

x + (x + 3) + 2x ≤ 91

4x + 3 ≤ 91

4x + 3 ≤ 91 - 3

$\Rightarrow x\le \frac{88}{4}$

x ≤ 22.

⸫ 8 ≤ x ≤ 22.

Hence the length of the shortest board is greater than or equal to 8 cm and less than or equal to 22 cm.

 

Exercise 6.2

Solve the following inequalities graphically in two-dimensional plane:

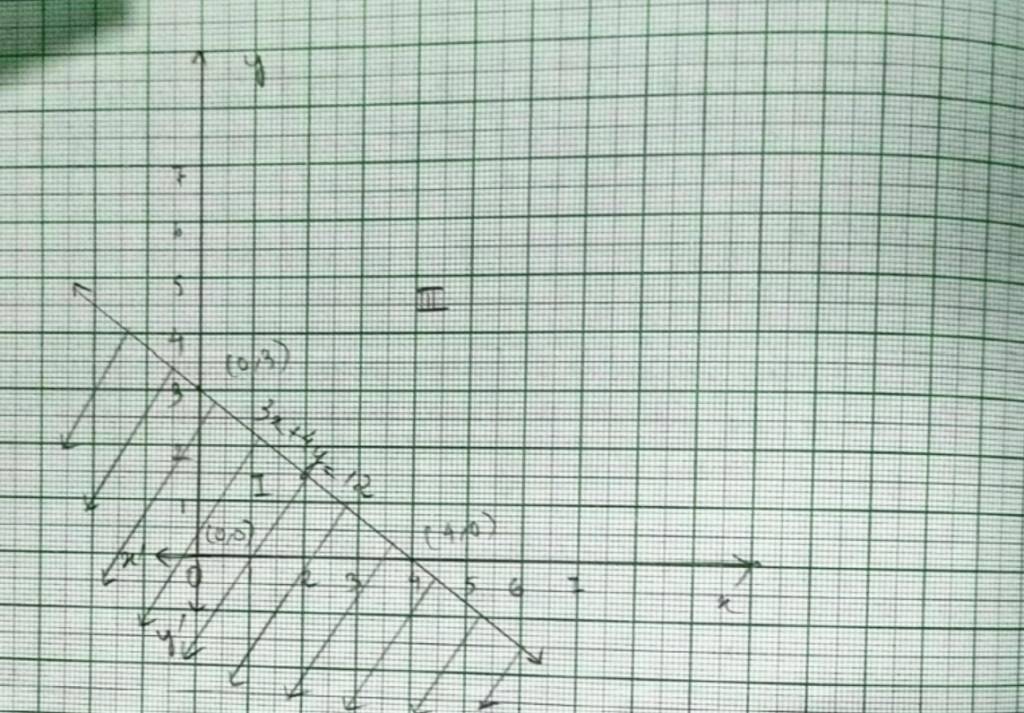
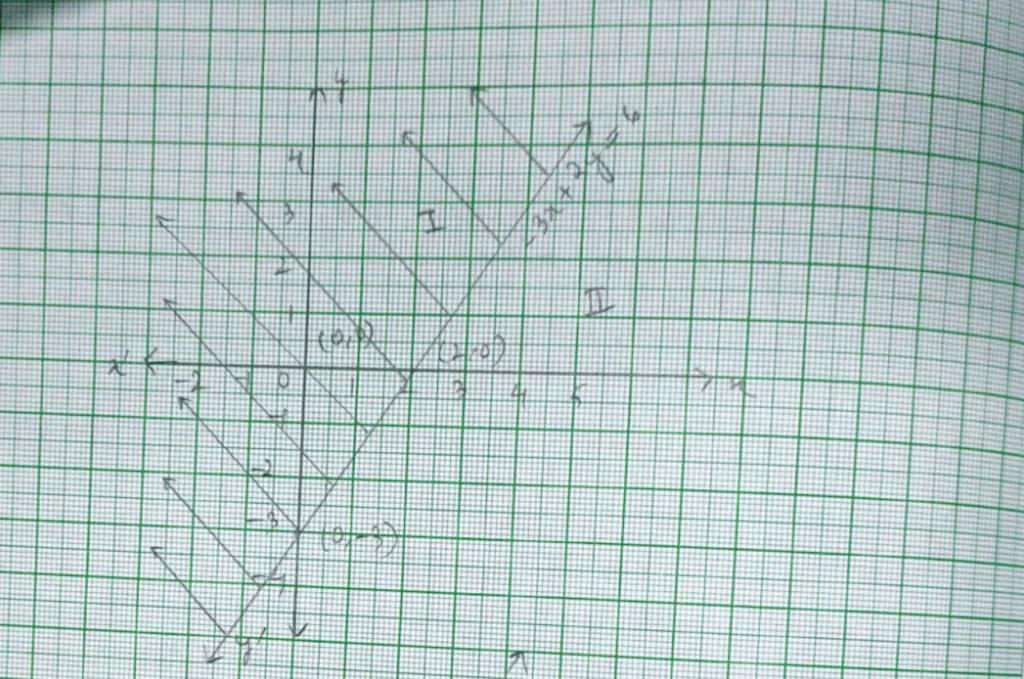
Q1. x + y < 5

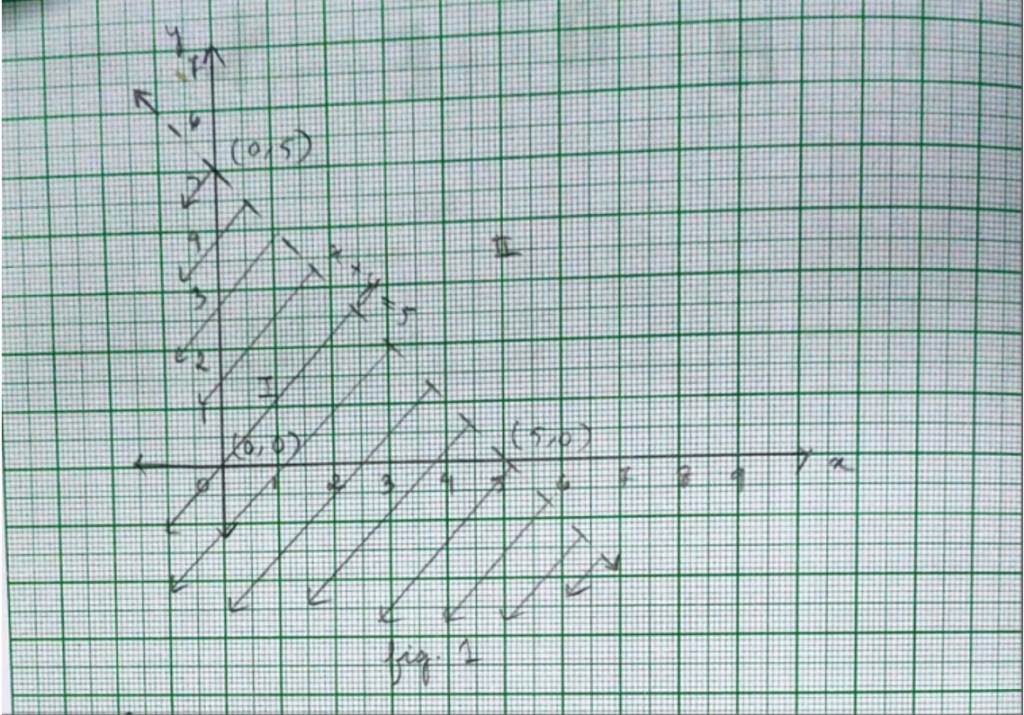
A.1. For inequality, x+y <5, the equation of line is x+y=5.

We consider the tableto plot x+y=5.

Graph of x+y=5 is given as dotted line in fig 1. This lines divides by plane in two half planes I and II. We select a point not on the line, say (0,0) which lies in region I.

Since, 0+0<5

0<5is true.

The solution region is I. (where origin (0,0) is included)

The dotted line indicates that any point on the line does not satisfy the given inequality.

 

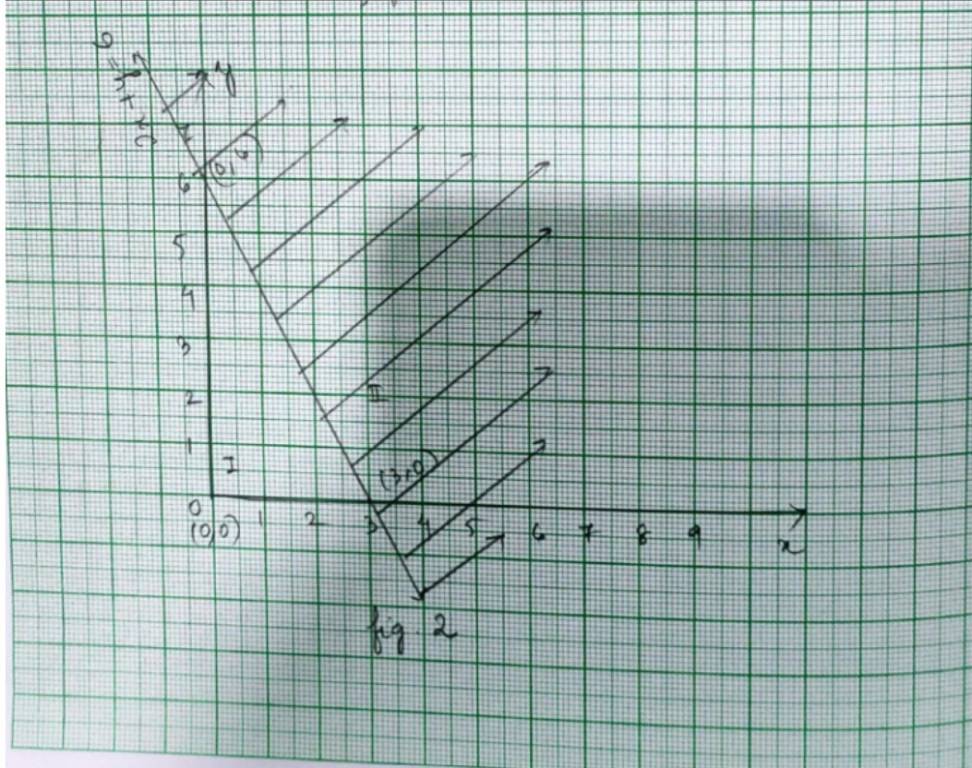
Q2. 2x + y ≥ 6

A.2. For inequality, 2x+y≥ 6, the equation of line is 2x+y=6.

We consider the table below to pot 2x+y=6.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ 6\end{array}|\begin{array}{l}3\\ 0\end{array}|$

Graph of 2x+y=6 is given as a continuous line in fig 2.

This line divides xy-plane in two half planes I and II.

We select 0(0,0) and check the correctness of the inequality.

is 2 × 0+0 ≥ 6.

0 ≥ 6 which is false.

So, the solution region is II where origin (0,0) is included.

The continuous line indicates that any point on the line. also satisfy the given inequality.

 

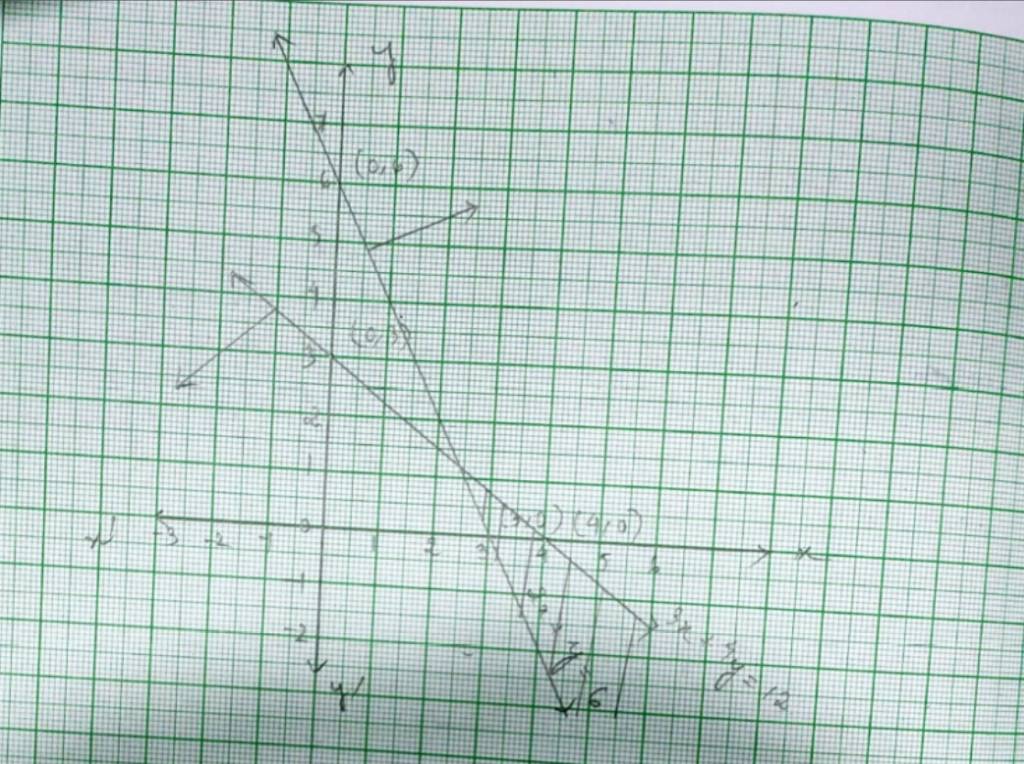
Q3. 3x + 4y ≤ 12

A.3. For inequality 3x+4y≥ 12 the equation of the line is 3x+4y=12

We consider the table below to plot 3x+4y=12.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ 3\end{array}|\begin{array}{l}4\\ 0\end{array}|$

This line devides the xy-plane into half planer I and II.

We select point 0(0,0) and check the correctness of the inequality.

i.e., 3 × 0+4 × 0 ≤ 12.

0+0 ≤ 12

0 ≤12 which is true.

So, the solution region is I which includes the origin (0,0). The continuous line also indicates that any points in the line also satisfy the given inequality.

 

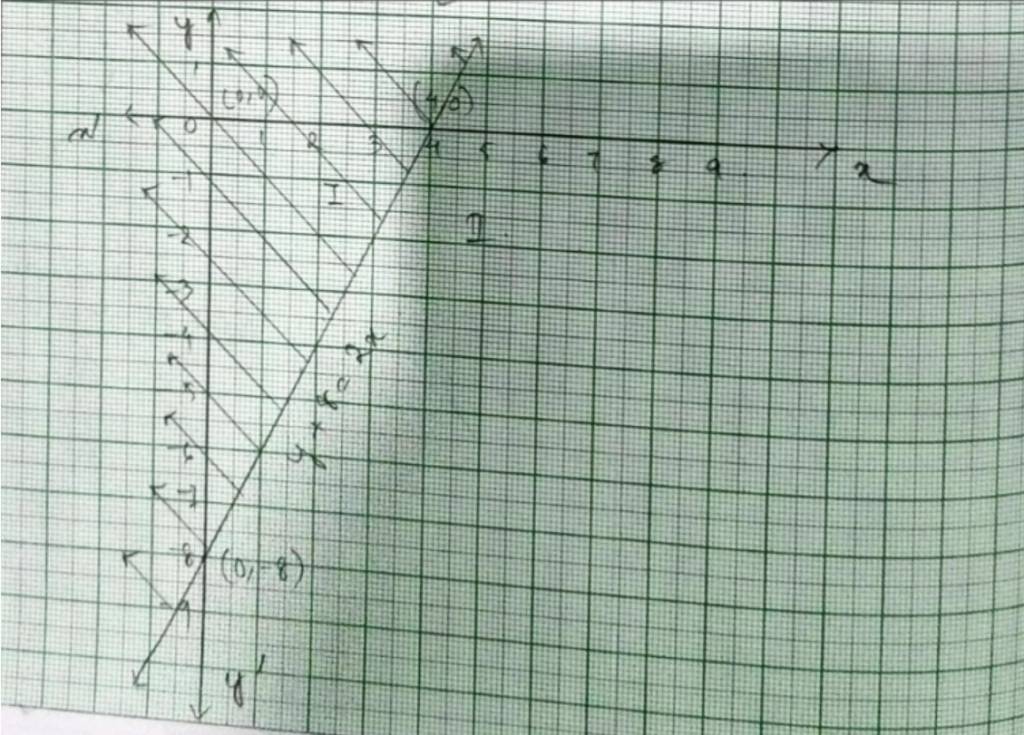
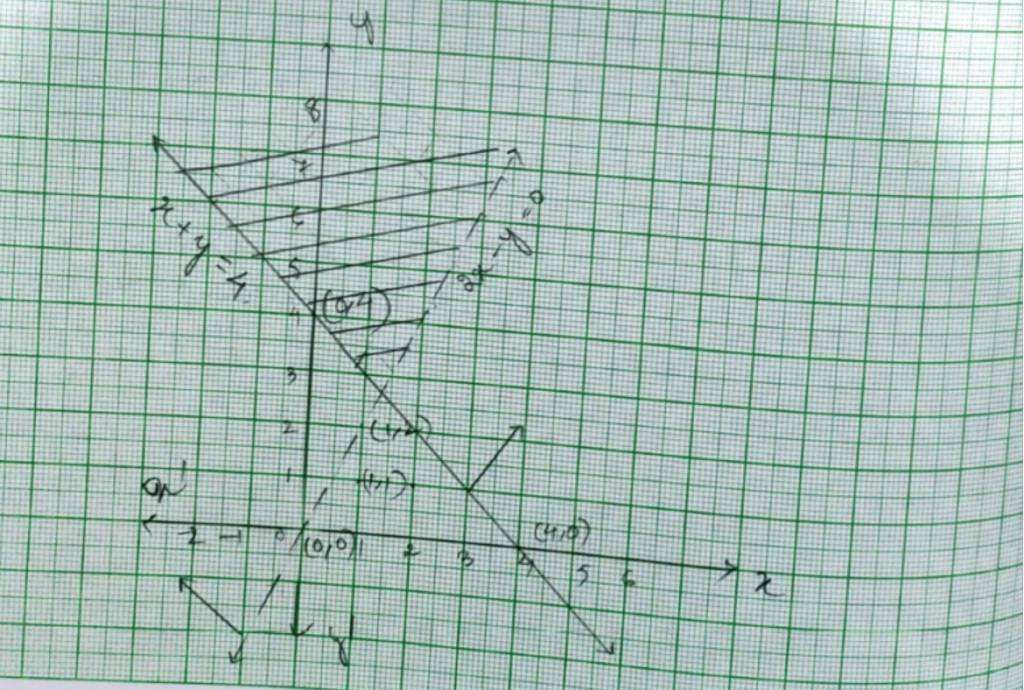
Q4. y + 8 ≥ 2x

A.4. For inequality y+8 ≤ 2x, the equation of the line is y+8=2x. We consider the table below to plot of y+8=2x.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ -8\end{array}|\begin{array}{l}4\\ 0\end{array}|$

The line devides the xy-plane into half planer I and II. We select a point (0,0) and check the correctness of the inequality.

i.e., 0+8 ≤ 2 × 0

0 ≤ 0 which is true.

So, the solution region is I which includes the rigin (0,0). The continuous line also indicates that any points on the line also satisfy the given inequality.

 

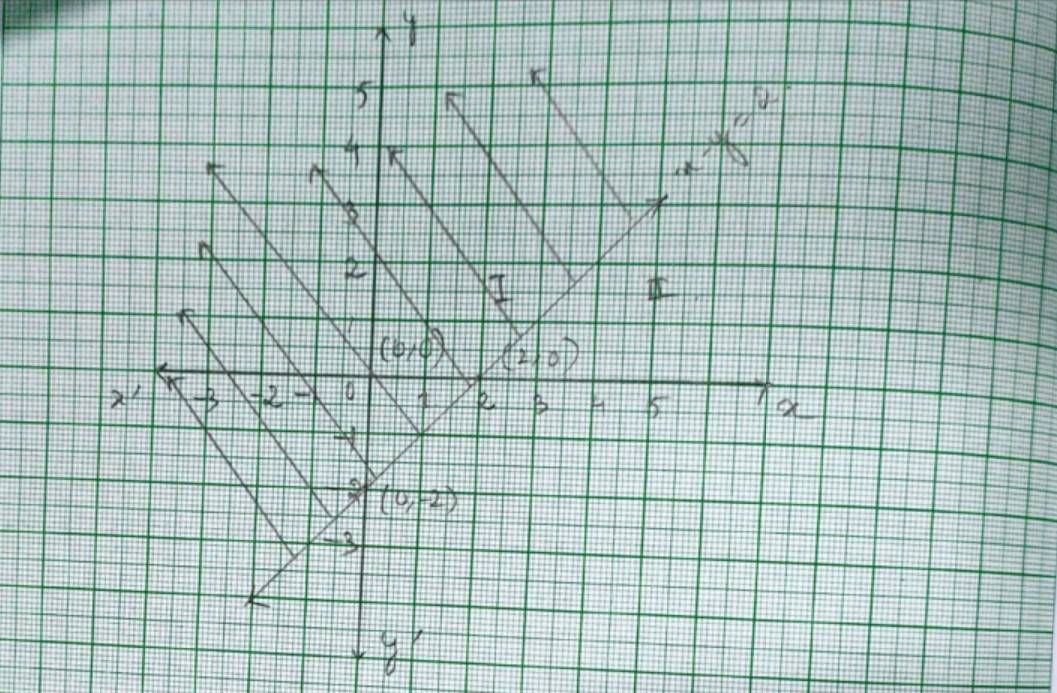
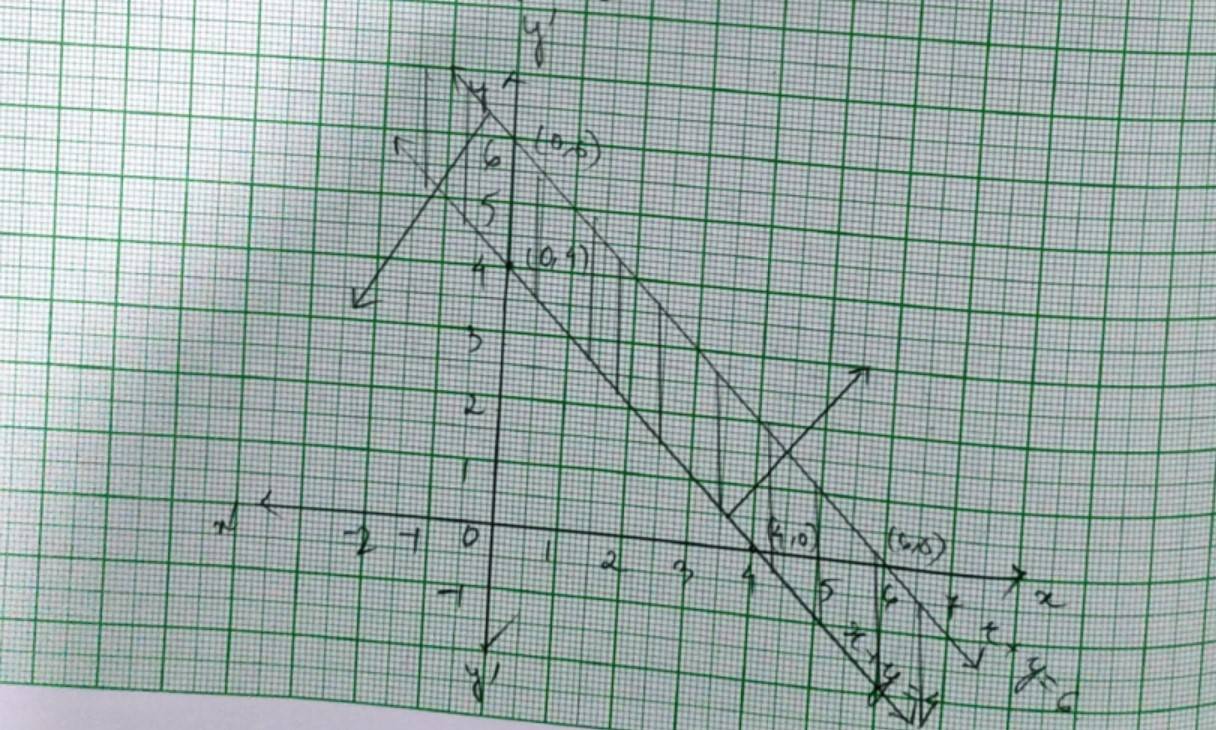
Q5. x – y ≤ 2

A.5. For the inequality x – y≤ 2 so the equation of line is x – y=2. We consider the table below to plat x – y=2

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ -2\end{array}|\begin{array}{l}2\\ 0\end{array}|$

This line divides the xy-plane into half planer I and II. We select point (0,0) and check the correctness of the inequality.

0 – 0 ≤ 2

0 ≤ 2 which is true.

So, the solution region is I which includes the origin (0,0). The continuous line also indicates that any point on the line also satisfy the given inequality.

 

Q6. 2x – 3y > 6

A.6. For the inequality, 2x – 3y>6 the eqⁿ is 2x – 3y=6. We consider the table below to plot 2x – 3y=6.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ -2\end{array}|\begin{array}{l}3\\ 0\end{array}|$

This line divides the xy-plane into half planer I and II. We select point (0,0) and check the correctness of the inequality.

2 × 0 – 3 × 0>6

0>6 which is false.

So, the solution region is II which does not includes the origin (0,0).

The dotted line indicates that the any point on the line does not satisfy the given inequality.

 

Q7. – 3x + 2y ≥– 6

A.7. For the inequality –3x+2y≥ –6 the equation of line is – 3x+2y=6.

We consider the table below to plot – 3x+2y= –6.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ -3\end{array}|\begin{array}{l}2\\ 0\end{array}|$

This line divides the xy-plane into two planer I and II. We select a point (0,0) and check the correctness the inequality,

–3 × 0+2 × 0 ≥ –6

0 ≥ –6 which is true.

So, the solution region is I which includes the origin. The continuous line also indicates that any point on the line also satisfy the given inequality.

 

Q8. 3y – 5x < 30

A.8. For the inequality 3y – 5x<30, the equation of line is 3y – 5x=30. We consider the table below to plot 3y – 5x =30.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ 10\end{array}|\begin{array}{l}-6\\ 0\end{array}|$

This line divides the xy-plane into two planer I and II. We select a point (0,0) and check the correctness the inequality.

3 × 0 – 5 × 0<30

0<30 which is true.

So, the solution region is I which includes the origin. The dotted line indicates that any point on the line will not satisfy the given inequality.

 

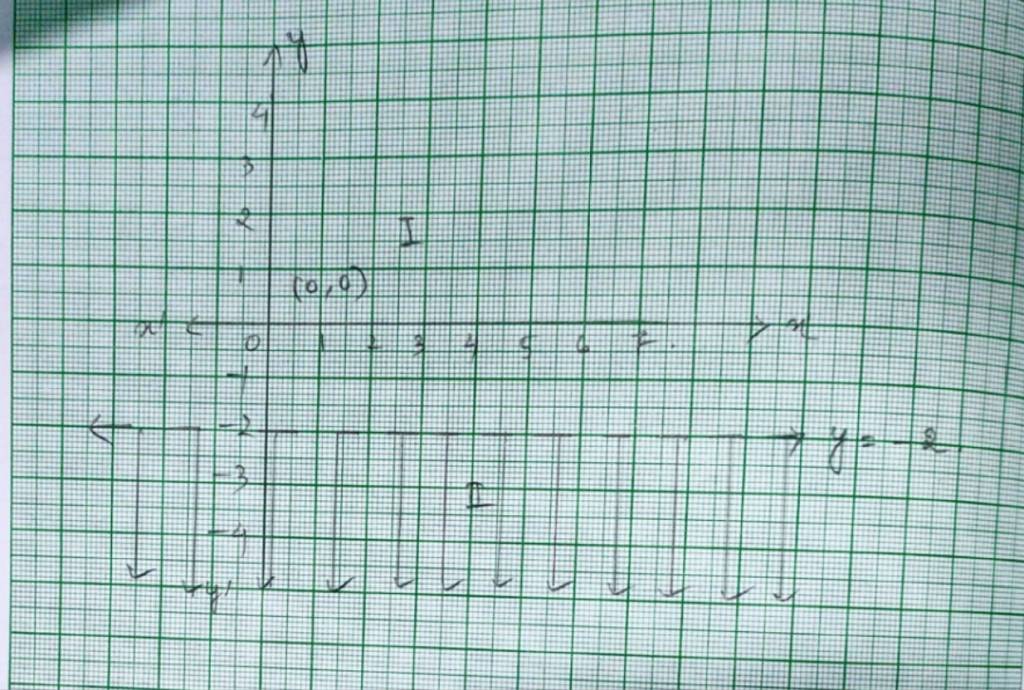
Q9. y < – 2

A.9. For the given equation inequality y< –2,

the equation of line is y= –2

This line devides the xy-plane into two planer I and II. We take a point (0,0) to check the correctness of the inequality.

So, 0< –2

0< –2 which is false.

So, the solution of the region is II which does not include the origin.

The dotted line indicates that any point on the line does not satisfy the inequality.

 

Q10. x > – 3

A.10. For the given inequality, x> –3.

the equation of the line is x= –3.

This line divides the xy-plane into planer I and II. We take a point (0,0) to check the correctness of the inequality.

So, 0> –3 which is true.

So, the solution of the region is I which includes the origin.

The dotted line indicates that any point on the line does not satisfy the inequality.

 

Ex. 6.3

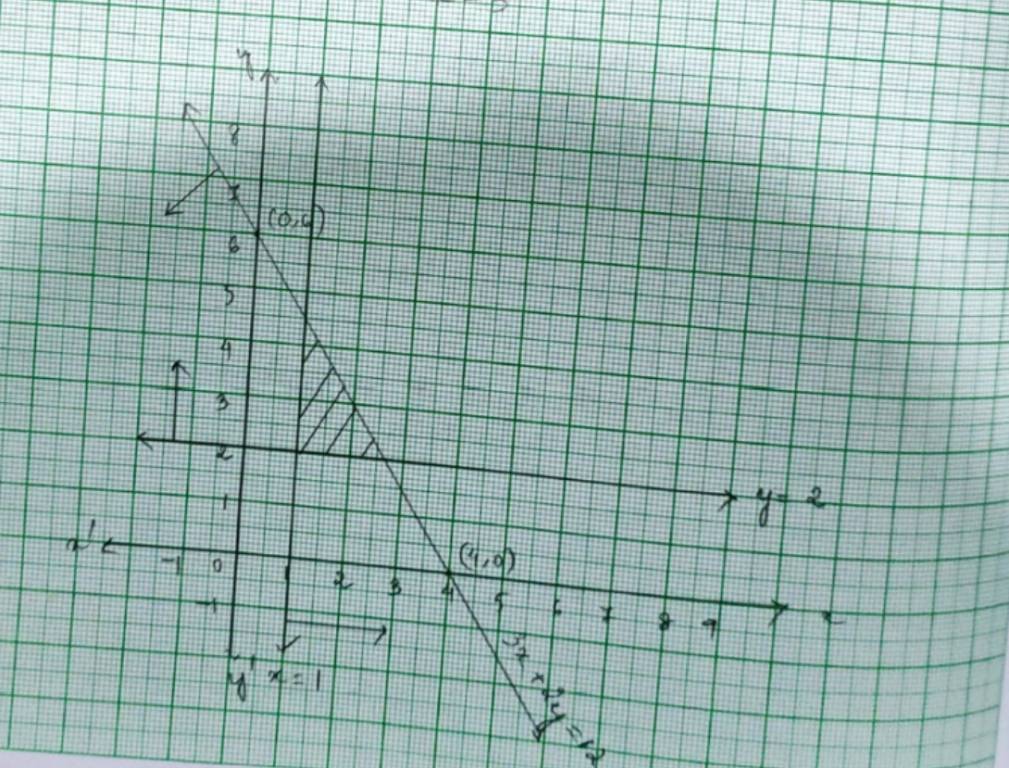
Q1. x ≥ 3, y ≥ 2

A.1. The given system of inequalities are.

x≥ 3 ------------(1)

y≥ 2 ------------(2)

We draw the graphs of the lines x=3 and y=2. The inequality (1) and (2) represent the region between the two lines, including the points on the respective lines. So, every point in the shaded region in first quadrant represents a solution of the given system of inequalities.

 

Q2. 3x + 2y ≤ 12, x ≥ 1, y ≥ 2

A.2. The given system of inequalities are

3x+2y≤ 12----------(1)

x≥ 1----------(2)

y≥ 2----------(3)

We draws the graphs of the lines 3x+2y=12 using points and as 3 × 0 + 2 × 0 ≤ 12

The solution is plane which includes the origin (0, 0).

0 ≤ 12

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ 6\end{array}|\begin{array}{l}4\\ 0\end{array}|$

and x = 1 and y = 2.

The inequality (1), (2) and (3) represents the region between these three lines including the points on the respective lines. So, every point on the shaded region in first quadrant represents a solution of the given system of inequalities.

 

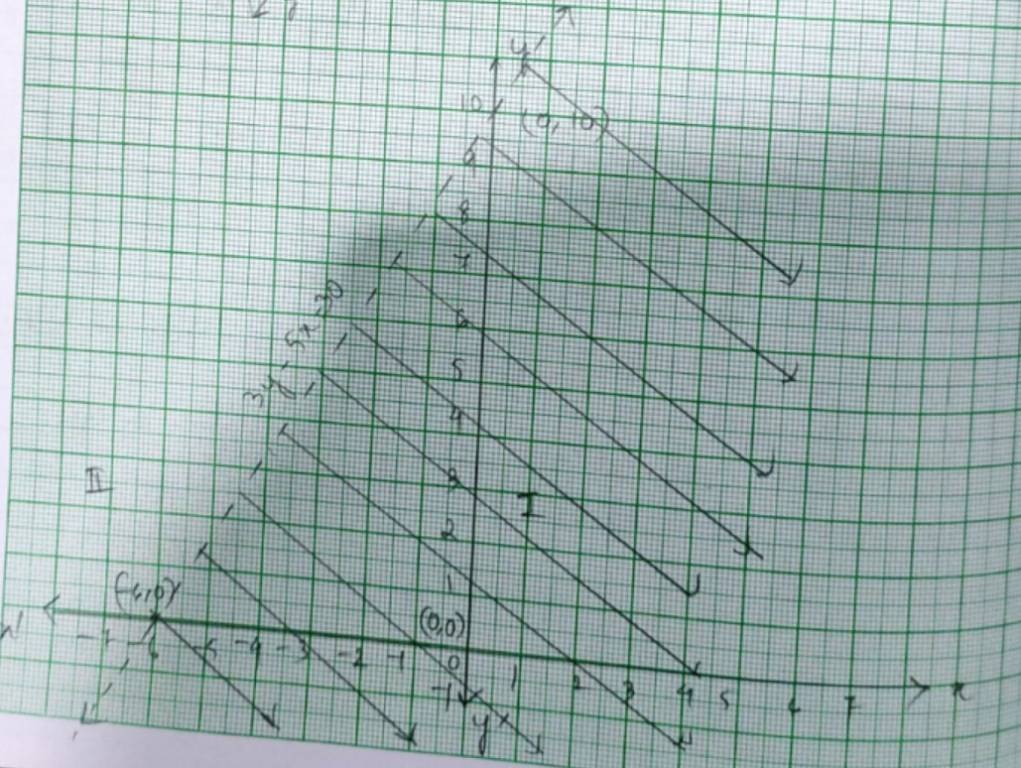
Q3. 2x + y ≥ 6, 3x + 4y < 12

A.3.The given system of inequalities is

2x+y≥ 6 ----------------------(1)

3x+4y≤ 12---------------------(2)

The corresponding equations are

2x + y = 6

Put (x, y)=(0,0) in (1),(2),

⸫ 2 × 0+0 ≥ 6

0 ≥ 6 which is false.

And 3 × 0+4 × 0 ≤ 12

0 ≤ 12 which is true.

So, solution of inequality (1) lies on the plane which excludes the origin and the solution of inequality (2) lies on the plane which includes the origin.

So, the required solution of the given system of inequality is the shaded region.

 

Q4. x + y ≥ 4, 2x – y < 0

A.4. The given system of inequalities is

x + y ≥ 4.---------------------(1)

2x – y< 0.---------------------(2)

The corresponding equations are x+y=4 and 2x – y=0.

x	0	4
y	4	0

            and

X	0	1
Y	0	2

 Put (x, y)=(1,1) in (1) and (2).

So, 1+1 ≥ 4

2 ≥ 4 which is not true.

and 2 × 1 – 1<0

1<0 which is not true.

So solution of plane of inequality (1) and (2) does not include the plane with point (1,1).

⸫ The reqd. solution of the given system of inequality is the shaded portion.

 

Q5. 2x – y >1, x – 2y < – 1

A.5.The given system of inequality is

2x – y> 1 -----------------(1)

x – 2y< –1-----------------(1)

So the corresponding equations are

2x – y=1

x	0	0.5
y	–1	0

and x – 2y= –1

x	–1	0
y	0	0.5

Putting (x, y)=(0,0) in (1) and (2) to cheek the inequality

2 × 0 – 0 > 1

0 > 1 which is not true.

and 0 – 2 × 0< –1

0< –1 which is not true.

So, the solution of plane of inequality (1)and (2) does not include the plane with point (0,0) or origin.

⸫ The reqd. solution of the given system of inequality is the shaded region.

 

Q6. x + y ≤ 6, x + y ≥ 4

A.6. The given system of inequality is

x+y≤ 6 ---------------(1)

x+y≥ 4---------------(2)

So the corresponding equations are

x+y=6

x	0	6
y	6	0

andx + y = 4

x	4	0
y	0	4

Putting (x, y)=(0,0) in equality (1) and (2),

0+0 ≤ 6     and 0 + 0 ≥ 4

0 ≤ 6 is true.            => 0 ≥ 4 is false.

So, solution of plane of inequality (1) includes the origin and inequality(2) does not includes the origin.

⸫The reqd solution of the given system of inequality is the shaded region.

 

Q7. 2x + y ≥ 8, x + 2y ≥ 10

A.7. Given system of inequality is

2x+y≥ 8-----------------(1)

x+2y≥ 10-----------------(2)

The corresponding equations are

2x + y = 8

x	0	4
y	8	0

and x + 2y = 10

x	10	0
y	0	5

Now, putting (x, y)=(0,0) in inequality (1) and (2),

2 × 0+8 ≥ 8

0 ≥ 8 which is not true.

and 0+2 × 0 ≥ 10

0 ≥ 10 which is not true.

So, solution of plane of inequality (1) and (2) does not include the origin (0,0)

⸫The required solution of the given system of inequality is the shaded region.

 

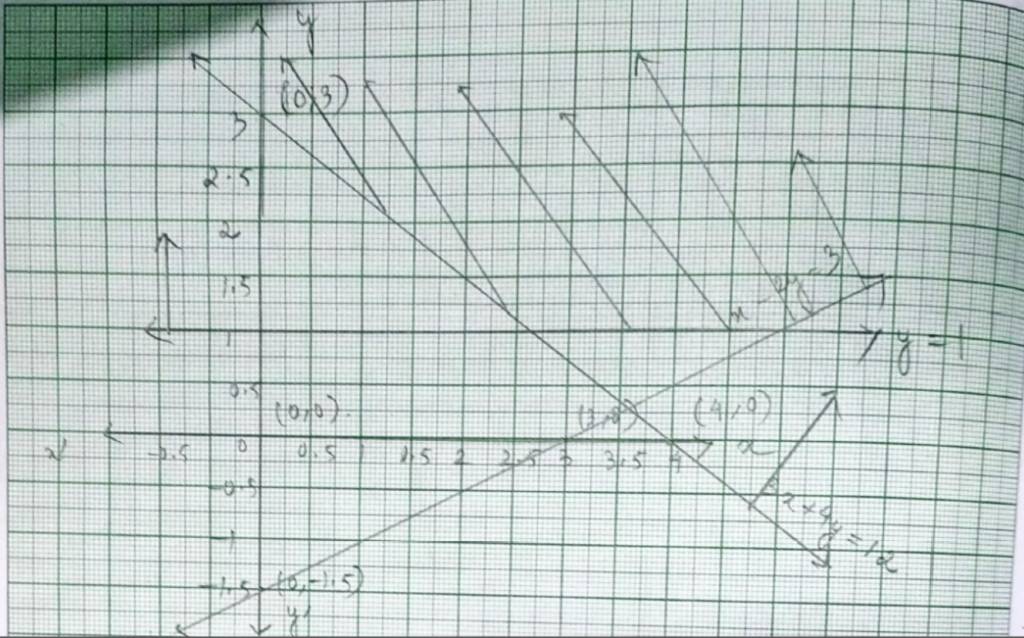
Q8. x + y ≤ 9, y >x, x ≥ 0

A.8.The given system of inequality is

x+y≤ 9-------------------(1)

y>x-------------------(2)

x≥ 0 -------------------(3)

The corresponding equation of (1) is x+y=9 and (2) is y=x

x	9	0
y	0	9

 

x	0	1
y	0	1

Substituting (x, y)=(0,0) in (1),

0+0 ≤ 9    => 0 ≤ 9 which is true.

And putting (1,0) in (2)

0> 1which is false.

So, solution region of inequality (1) includes origin (0,0) and solution region of inequality (2) excludes plane having (1,0).

⸫Solution of region of given system of inequality is the shaded region.

 

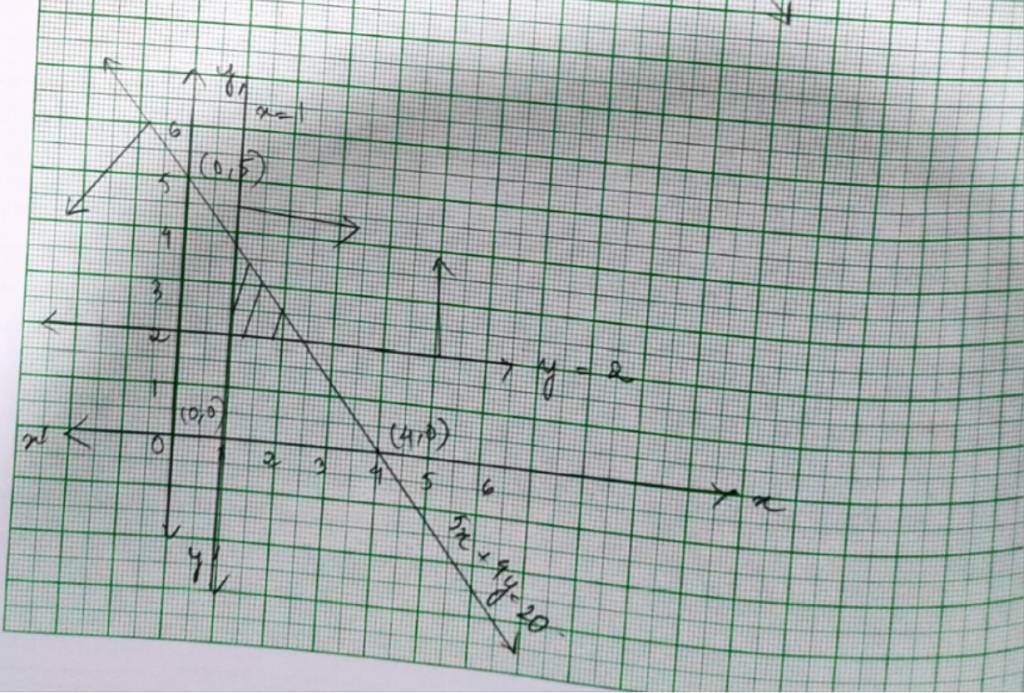
Q9. 5x + 4y ≤ 20, x ≥ 1, y ≥ 2

A.9. The given system of inequality is

5x+4y≤ 20 -----------------------(1)

x≥ 1 -----------------------(2)

and  y≥ 2 -----------------------(3)

The equation of inequality (1) is 5x+4y=20.

x

4

0

y

0

5

Putting (x, y)=(0,0) in inequality (1) we get,

5 × 0+4 × 0 ≤ 20   => 0 ≤ 20 which is true.

So, the solution region of inequality (1) includes the plane with origin (0,0).

⸫The shaded region indicates the solution of the given system of inequality.

 

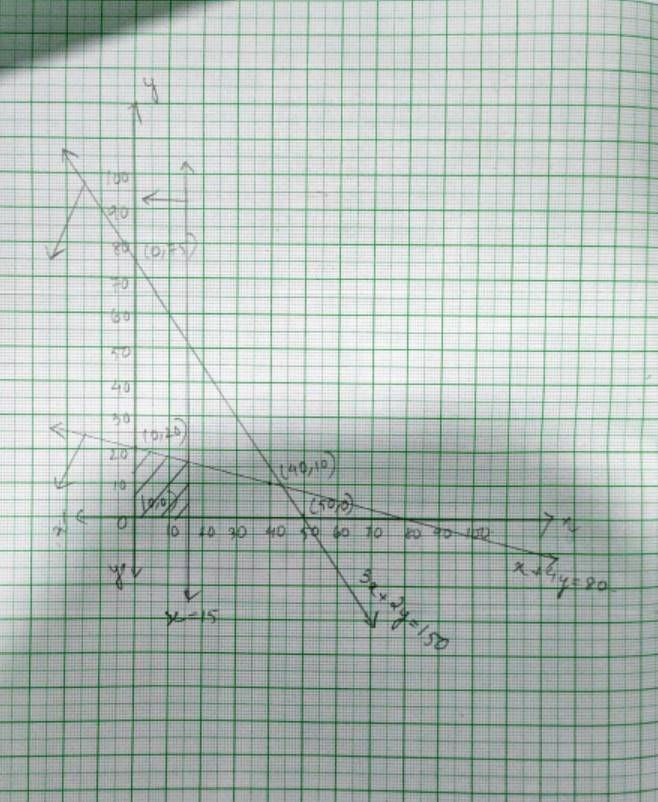
Q10. 3x + 4y ≤ 60, x +3y ≤ 30, x ≥ 0, y ≥ 0

A.10. The given system of inequality is

3x+4y ≤ 60 -------------------(1)

x+3y ≤ 30-------------------(2)

x≥ 0 -------------------(3)

xy≥ 0 -------------------(4)

The corresponding equation of (1) and (2) are

3x + 4y = 60

x	20	0
y	0	15

and   

x + 3y = 30

x	0	30
y	10	0

Putting (x, y)=(0,0) in equality (1) and (2),

3 × 0+4 × 0 ≤ 60 and 0+3 × 0 ≤ 30

0 ≤ 60 which is true and 0 ≤ 30 which is true

So, the solution plane of inequality (1) and (2) is the plane including origin (0,0)

⸫The shaded portion is the solution of the given system of inequality.

 

Q11. 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6

A.11.The given system of inequality is

2x + y ≥ 4---------(1)

x + y ≤ 3---------(2)

2x – 3y ≤ 6---------(3)

The corresponding equation are

2x + y = 4

x	2	0
y	0	4

and

x + y = 3

x	0	3
y	3	0

and

2x + 3y = 6

x	3	0
y	0	–2

Putting (x,y)=(0,0) in (1), (2) and (3),

2 × 0+0 ≥ 4

0 ≥ 4 which is false.

and 0+0 ≤ 3   => 0 ≤ 3 which is true.

and 2 × 0 – 3 × 0 ≤ 6  => 0 ≤ 6which is also true.

So, solution of inequality (1) excludes plane with origin while solution of inequality (2) and (3) includes the plane with origin.

⸫The shaded portion is the reqd. solution of the given system of inequality.

 

Q12. x – 2y ≤  3, 3x + 4y ≥ 12, x ≥ 0 ,y ≥ 1

A.12. The given system of inequality is

x – 2y≤ 3 ------------(1)

3x – 4y≥12------------(2)

x ≥ 0 ------------(3)

y≥ 1 ------------(4)

The corresponding equation of (1) and (2) are

x – 2y= 3

x	3	0
y	0	–1.5

and 3x – 4y=12

x	4	0
y	0	3

Putting (x, y)=(0,0) in inequality (1) and (2),

0 – 2 × 0 ≤ 3   => 0 ≤ 3 is true.

and 3 × 0+4 × 0 ≥ 12   => 0 ≥ 12 is false.

So, solution of inequality (1) includes plane wilt origin (0,0) while solution plane of inequality (2) includes the origin.

⸫The shaded portion determines the solution region of the given system of inequality.

 

Q13. 4x + 3y ≤  60, y ≥ 2x, x ≥ 3, x, y ≥ 0

A.13. The given system of inequality is

4x+3y≤ 60-----------(1)

y≥ 2x------------(2)

x≥ 3------------(3)

andx, y ≥ 0------------(4)

The corresponding equation of inequality (1) and (2) are

4x+3y= 60

x	0	15
y	20	0

and y = 2x

x	0	1	2
y	0	2	4

Putting (1,0) in inequality (1) and (2) we get,

4 × 1+3 × 0 ≤ 60

4 ≤ 60 which is true.

and 0 ≥ 2 × 1

0 ≥ 2 which is false.

So, solution of inequality (1) includes the plane with point (1,0) whereas the solution of inequality (2) excludes the plane with point (1,0).

⸫The shaded region is the solution of the given system of inequality.

 

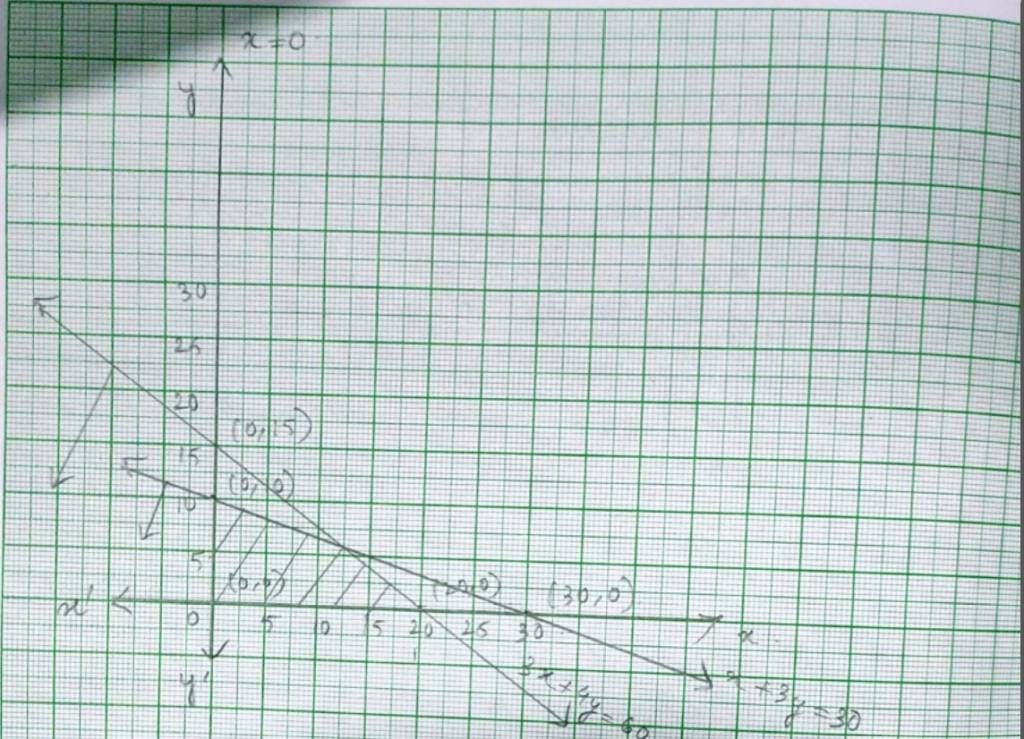
Q14. 3x + 2y ≤ 150, x + 4y ≤  80, x ≤ 15, y ≥ 0, x ≥ 0

A.14.The given system of inequality is

3x+2y≤ 150-------------(1)

x+4y≤ 80-------------(2)

x≤ 15 -------------(3)

y≥ 0 and x≥ 0 -------------(4)

The corresponding equation of (1) and (2) are

3x + 2y = 150

x	50	0
y	0	75

and x + 4y =80

x	0	40
y	20	10

Putting (0,0)=(x, y) in inequality (1) and (2) we get,

3 × 0+2 × 0 ≤ 150  => 0 ≤ 150 is true.

and 0+4 × 0 ≤ 80  => 0 ≤ 80 is true.

So, the solution plane of both inequality (1) and (2) includes the origin (0,0).

⸫The shaded region is the solution of the given system of inequality.

 

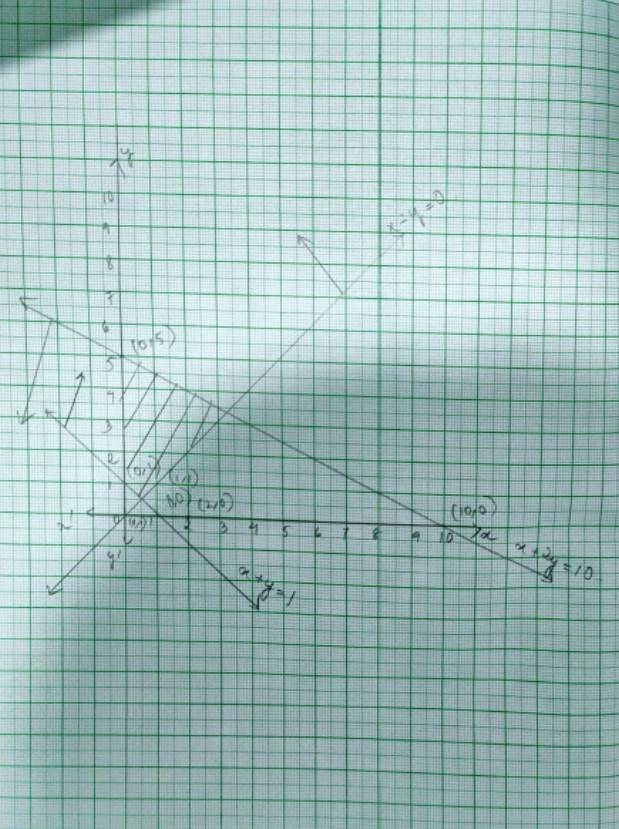
Q15. x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0

A.15. The given system of inequality is

x+2y≤ 10-------------(1)

x+y≥ 1 -------------(2)

x – y ≤ 0 -------------(3)

x≥ 0 and y≥ 0 -------------(4)

The corresponding equation of (1), (2) and (3) are

x + 2y = 10

x	0	10
y	5	0

and x + y =1

x	0	1
y	1	0

and x – y = 0

x	0	1
y	0	1

Putting (2,0)=(x, y) in inequality (1), (2) and(3),

2+2 × 0 ≤ 10 =>  2≤ 10 is true.

and 2+0 ≥ 1 =>  2 ≥ 1 is true.

and 2 – 0 ≤ 0  => 2 ≤ 0 is false.

So, the solution of inequality (1) and (2) is the plane which includes point (2,0) whereas the solution of inequality (3) is the plane which includes point (2, 0)

⸫The shaded region represents the solution of the given system of inequality.