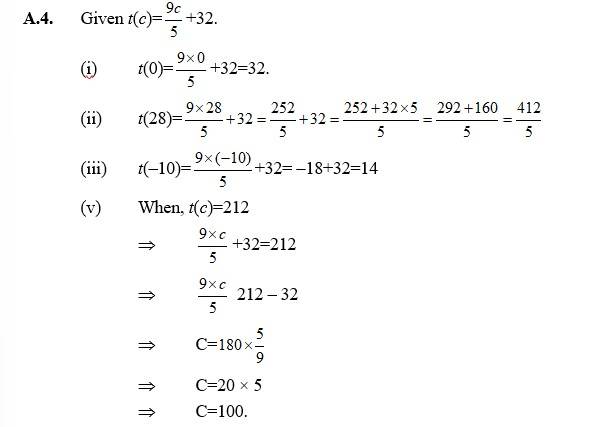Class 11 Maths NCERT Solutions Chapter 2 Relations and Functions: Topics, Questions, Preparation

Class 11 Math Chapter 1 Relation and Function carries 6-10 marks weightage in the annual exams. Chapter 2 Relation and Function is also important to understand complex JEE Mains topics such as calculus and inverse trigonometry. Students can check several key topics are discussed in the exercises; 

Class 11 Relation and Function Key Topics

• Relations and Cartesian Product of Sets: Ordered pairs, Cartesian product of two sets (A × B), Representation of relations
• Types of Relations: Empty Relation, Universal Relation, Symmetric Relation, Transitive Relation, Reflexive Relation, and Equivalence Relation.
• Functions and Their Representation; Definition of a function, Domain, co-domain, and range
• Types of Functions; One-One, Onto, Bijective, and into functions

Relation and Function Important Formulae for CBSE and Competitive Exams

Number of Relations:

$$2^{mn}, \quad \text{where } A \text{ has } m \text{ elements and } B \text{ has } n \text{ elements}$$

Number of Functions:

$$n^m, \quad \text{(A has m elements, B has n elements)}$$

One-One Function Condition:

• $f(x_1) = f(x_2) \Rightarrow x_1 = x_2$

Students can find the solutions to all the exercises of class 11 relation and function in one place compiled by our experts. This class 11 Relation and Function NCERT solution PDF is very useful for all categories of students whether on boards or competitive exams. access the PDF below;

Class 12 Math Chapter 1 Relation and Function Solution: Free PDF Download

The class 11 Relation and Function chapter 1 exercises deal with many important topics, such as relations and function basics, type of relations, symmetric and asymmetric relations, functions, their domain, and ranges. Students will encounter problems related to different concepts and properties of relations and functions in the exercises.  Candidates can check the exercise-wise Chapter 2 Relation and Function Exercise-wise solutions below;

Class 11 Relation and Function Exercise 2.1 focuses on fundamental concepts such as the introduction of relations, definition, ordered pairs, and the Cartesian product of sets. This chapter develops an understanding of how elements from two sets are paired and how different types of relations are formed. Class 11 Relation and Function Exercise 2.1 will consist of 10 solved Questions in simple language. Students can check the complete solutions of exercise 2.1 below;

Class 11 Math Chapter 2 Relation and Function Exercise 2.1 solutions

Q2. If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A×B).

A.2. Given, n(A) = 3

n(B) = 3 or B = {3,4,5}

So, number of elements in A× B = n(A× B) = n(A)× n(B) = 3 ×3 = 9.

Q3. If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.

A.3. Given, G = {7, 8} and H = {5, 4, 2}

By the definition of the Cartesian product,

G ×H = {(x, y): x∈G and y = ∈ H}

= {((7, 5), (7, 4), (7, 2), (8, 5),(8,4), (8,2)}

H× G = {(x, y): x∈ H and y ∈G}

= {(5, 7), (5, 8), (4,7), (4, 8), (2, 7), (2,8)}

Q4. State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.

(i) If P = {m, n} and Q = { n, m}, then P × Q = {(m, n),(n, m)}.

(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x  $\in$ A and y  $\in$ B.

(iii) If A = {1, 2}, B = {3, 4}, then A ×  $($  B   ∩   ϕ   )   =   ϕ  .

A.4. (i) False. Here P = {m, n}, n(p)=2

Q = {n, m}, n(Q)=2

n(P× Q) = n(P)× n(Q) = 2× 2 = 4.

So, P ×Q = {((m, n),(m, m),(n, n),(n, m)}

(ii) True.

(iii) True. { A ×(B   ∩   ϕ ) = A× ϕ  . { ∵ B ∩   ϕ = ϕ   }

= n(A) ×0 {∵ ϕ   is empty set}

= ϕ  

Q5. If A = {–1, 1}, find A × A × A.

A.5. Given, A = {1,1}

So, A× A = {(1,1),(1,1),(1,1),(1,1)}

A ×A ×A = {(1,1),(1,1),(1,1),(1,1)} ×{1,1}

= {(1,1.1),(1, 1, 1),(1, 1, 1,),(1,1,1), (1,1,1), (1, 1,1), (1, 1,1), (1,1,1)}

Q6. If A × B = {(a, x),(a , y), (b, x), (b, y)}. Find A and B.

A.6. Given,

A ×B = {(a, x),(a, y),(b, x),(b, y)}

We know that,

A ×B = {(p, q); p ∈ A and q ∈ B}

So, A = {a, b} and B = {x, y}.

Q7. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that (i) A × (B∩ C) = (A × B)∩ (A × C). (ii) A × C is a subset of B × D.

A.7.Given,

A={1, 2}, B = {1,2,3,4}, C={5,6} and D={5,6,7,8}

(i)L.H. S = A ×(B∩ C) = {1,2} [{1,2,3,4} ∩{5,6}]

={1,2}× ϕ  

= ϕ  .

R.H.S = (A× B)∩ (A ×C)=[{1,2}×{1,2,3,4}]∩[{1,2} {5,6}]

=[{(1 , 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)]∩ [{1,5),(1,6),(2,5), (2,6)}]

= ϕ  .

Hence, L.H.S= R.H.S.

(ii)

A× C ={1, 2}× {5,6}

={(1,5),(1,6),(2,5),(2,6)}

B× D ={1,2,3,4} ×{5,6,7,8}

={(1,5),(1,6),(1,7),(1,8),(2,5),(2,6),(2,7),(2,8),(3,5),(3,6),(3,7),(3,8),(4,5),(4,6),(4,7),(4,8)}

As every element of A C is also an element of B× D.

A ×C  $\subset$ B ×D

Q8. Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.

A.8. A Given, A={1,2}

B={3,4}

So, A× B={(1,3),(1,4),(2,3),(2, 4)}

i.e., n(A ×B)=4

A ×B will have subset =2⁴=16.They are,

Φ,{(1,3)},{(1,4)},{(2, 3)},{(2,4)},{(1,3),(1,4)},{(1,3),(2,3)},

{(1,3),(2, 4)},{(1,4),(2, 3)},{(1,4),(2, 4)}, {(2,3),(2, 4)},

{(1,3),(1,4),(2, 3)},{(1,3),(1,4),(2,4)}, {(1,3),(2,3),(2, 4)},{(1,4),(2,3),(2,4)},

and {(1,3),(1,4),(2,3),(2,4)}

Q9. Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.

A.9. Given, n(A)=3

n(B)= 2

So, n(Ax B)=n(A).n(B)=3x 2=6

as (x, 1),(y, 2),(z, 1) ∈Ax B={(x, y), x∈Aand y∈B}.

A={x, y, z} and B={1,2}

As n(A) = 3as n(B) = 2

Q10. The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0,1). Find the set A and the remaining elements of A × A.

A.10. Given, n(A × A)=9

n(A) ×n(A) = 9.

n(A)² = 3².

n(A) = 3 .

And (–1,0),(0,1)  $\in$ A × A i.e., A × A = {(x, y), x  $\in$ A, y  $\in$ B}

⸫A={–1,0,1}

And A × A={–1,0,1} × {–1,0,1}

={(–1, –1),( –1,0),( –1,1),(0, –1),(0,0),(0,1),(1, –1),(1,0),(1,1)}

Class 11 Math Relation and Function Exercise 2.2 focuses on different types of relations, including reflexive, symmetric, transitive, and equivalence relations. The Relation and Function Exercise 2.2 deals with application of the concepts of relations in real-world-based problem-solving.   Class 11 Math Chapter 2 Relation and Function Exercise 2.2 consists of 9 Questions. Students can check the solutions below;

Q1. Let A = {1, 2, 3,...,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y $\in$ A}. Write down its domain, co-domain and range.

A.1. Given,A ={1,2,3, …, 14}

R ={(x, y): 3x – y = 0; x, y  $\in$ A}

={(x, y): 3x = y; x, y  $\in$ A}.

= {(1,3),(2,6),(3,9),(4,12)}

Domain of R is the set of all the first elements of the ordered pairs in R

So, domain of R={1,2,3,4}

Codomain of R is the whole set A.

So, codomain of R={1,2,3, …, 14}

Range of R is the set of all the second elements of the ordered pains in R.

So, range of R={3,6,9,12}

Q2. Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y $\in$ N}. Depict this relationship using roster form. Write down the domain and the range.

A.2. Given,R ={(x, y): y = x + 5, x is a natural number less than 4; x, y $\in$ N}

={(x, y): y = x + 5; x, y  $\in$ N and x < 4}.

={(1,1+5), (2,2+5), (3,3+5)}

={(1,6), (2,7), (3,8)}

So, domain of R = {1,2,3}

range of R = {6,7,8}

Q3. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x $\in$ A, y  $\in$ B}. Write R in roster form.

A.3. Given,A={1,2,3,5}

B={4,6,9}

R={(x, y) : the difference of x & y is odd; x  $\in$ A, y  $\in$ B}.

={(x, y):|x – y| is odd and x  $\in$ A, y  $\in$ B}

={(1,4),(1,6),(2,9),(3,4),(3,6),(5,4),(5,6)}.

Q4. The Fig 2.7 shows a relationship between the sets P and Q. Write this relation

(i) in set-builder form (ii) roster form. What is its domain and range?

A.4. As R is a relation from set P to Q.

(i)R = {(x, y): x – 2 = y ; 5 ≤ x ≤ 7}

(ii)R = {(5,3),(6,4),(7,5)}

Domain of R={5,6,7}

range of R={3,4,5}

Q5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a , b $\in$ A, b is exactly divisible by a}.

(i) Write R in roster form

(ii) Find the domain of R

(iii) Find the range of R.

A.5. Given, A={1,2,3,4,6}

R={(a, b): a, b  $\in$ A, b is exactly divisible by a}

(i)R={(1,1),(1,2),(1,3),(1,4),(1,6),(2,2),(2,4),(2,6), (3,3),(3,6),(4,4),(6,6)}

(ii)Domain of R={1,2,3,4,6}

(iii)Range of R={1,2,3,4,6}

Q6. Determine the domain and range of the relation R defined by R = {(x, x + 5) : x $\in$ {0, 1, 2, 3, 4, 5}}.

A.6. Given,R ={(x, x+5): x $\in$ {0,1,2,3,4,5}}

={(0,0+5), (1,1+5), (2,2+5), (3,3+5), (4,4+5), (5,5+5)}

={(0,5),(1,6),(2,7),(3,8),(4,9),(5,10)}

So, domain of R={0,1,2,3,4,5}

range of R={5,6,7,8,9,10}

Q7. Write the relation R = {(x,x³) : x is a prime number less than 10} in roster form.

A.7. GivenR={(x, x³) : x is a prime number less than 10}

R ={(x, x³) : x = 2,3,5,7}

={(2,2³),(3,3³),(5,5³),(7,7³)}

={(2,8),(3,27),(5,125),(7,343)}

Q8. Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.

A.8. Given, A={x, y, z}so, n(A)=3

B={1,2} so n(B)=2

⸫ n(A × B)=n(A) ×n(B)=3 × 2=6

Hence, no. of relation from A to B=Number of subsets of A × B

=2⁶

=64.

Q9. Let R be the relation on Z defined by R = {(a,b): a, b $\in$ Z, a – b is an integer}. Find the domain and range of R.

A.9. Given,R={(a, b): a, b $\in$ z and a – b is an integer}

We know that, the difference of two integers is also an integer.

R={(a, b): a – b  $\in$ z & a, b  $\in$ z}

Domain of R=Z.

Range of R= Z.

Class 11 Math Chapter 2 Relation and Function Exercise 2.3 introduces the concept of functions, their definition, and how they differ from general relations. This exercise helps students understand important terms like domain, co-domain, and range while exploring different types of functions. Chapter 2 Relation and Function Exercise 2.3 consists of 5 solved questions. Students can check complete solutions below;

Class 11 Math Chapter 2 Relation and Function Exercise 2.3 Solutions

Q1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.

(i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}

(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}

(iii) {(1,3), (1,5), (2,5)}.

A.1. (i)Domain of the given relation ={2,5,8,11,14,17}

Since every element of the domain has one and only one image, the given relation is a fxⁿ.

So, domain ={2,5,8,11,14,17}

range ={1}

(ii)Domain of the given relation ={2,4,6,8,10,12,14}

Since every element of the domain has one and only one image, the given relation is a fxⁿ.

So, domain = {2, 4, 6, 8, 10, 12, 14}

range ={1,2,3,4,5,6,7}

(iii)Domain of the given relation ={1,2}

As element 1 has more than one image i.e., 3 and 5, the given relation is not a fxⁿ.

Q3. A function f is defined by f(x) = 2x –5. Write down the values of

(i) f (0), (ii) f (7), (iii) f (–3).

A.3. Give, f(x) = 2x – 5.

(i)f(0)=(2 × 0) –5=0 – 5= –5

(ii)f(7)=(2 × 7) –5=14 – 5=9

(iii)f(–3)=2 ×(–3) –5= –6 – 5= –11.

Q4. The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C) = $\frac{9}{}$  C / 5   +   3   2  .

Find (i) t(0) (ii) t(28) (iii) t(–10) (iv) The value of C, when t(C) = 212.

Q5. Find the range of each of the following functions.

(i) f (x) = 2 – 3x, x  $\in$ R, x > 0.

(ii) f (x) = x²+ 2, x is a real number.

(iii) f (x) = x, x is a real number.

A.5. (i)f(x)=2 – 3x, x $\in$ R, x>0.

Given, x>0

3x>3 × 0

3x>0

(–1) × 3x<(–1) × 0.

–3x<0

2 – 3x<0+2

2 – 3x<2

i.e., f(x) < 2

Hene, range of f(x) = (– ꝏ, 2)

(ii)Given, f(x) = x²+2, x is a real number.

Since, x is a real number,

x² ≥ 0 (x²=0 for x=0)

x²+2 ≥ 0+2

x²+2 ≥ 2

f(x) ≥ 2

⸫Range of f(x) = [2, ꝏ) 

(iii)Given, f(x) = x, x is a real number.

As, f(x) = x, the range of f(x) is also real.

i.e., Range of f(x) = R.

Class 11 Math Chapter 2 Miscellaneous Exercise brings together all fundamental and advanced concepts of relations and functions such as types of relations, different functions, domain and range, and function composition. Miscellaneous Exercise of Class 11 Chapter 2 will contain Solutions 12 Questions. Students can check the complete solution below;

Class 11 Math Chapter 2 Relation and Function Exercise 2.1 solutions

f(x) ≥ 0

So, range of f(x)=[0, ꝏ)

Q5. Find the domain and the range of the real function f defined by $f$  (   x   )   =   |   x   −   1   |  .

A.5. Given, f(x)=|x – 1|.

The given function is defined for all real number x.

Hence, domain of f(x)=R.

As f(x)=|x – 1|, x  $\in$ R is a non-negative no.

Range of f(x)=[0, ꝏ), if positive real numbers.

Q7. Let f, g : R→R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and $\frac{f}{}$  g  .

A.7. Given, f(x) = x+1. and g(x) = 2x – 3.

So, (f +g)(x) = f(x)+g(x) = (x+1)+(2x – 3) = x+1+2x – 3 = 3x – 2

(f – g)(x) = f(x) –g(x) = (x+1)–(2x–3) = x+1 – 2x+3 = 4 – x

$\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}=\frac{x+1}{2x-3} such that x\ne \frac{3}{2}$

Q8. Let f = {(1,1), (2,3), (0,–1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.

A.8.  Given, f(x) = (ax + b)

= {(1,1),(2,3),(0, – 1),(–1, –3)} .

As (1,1)  $\in$ f.

Then, f(1)=1   [⸪ f(x) = y for (x, y)]

a × 1+b=1

a+b=1…… (1)

and (0, – 1)  $\in$ f .

Then, f(0)= –1

a× 0+b= –1

b= –1……..(2)

Putting value of (2) in (1) we gets

a – 1=1

a=1+1

a=2

So, (a, b)=(2, –1)

Q9. Let R be a relation from N to N defined by R = {(a, b) : a, b $\in$ N and a = b²}. Are the following true?

(i) (a,a)  $\in$ R, for all a _ N (ii) (a,b)  $\in$ R, implies (b,a)  $\in$ R

(iii) (a,b)  $\in$ R, (b,c)  $\in$ R implies (a,c)  $\in$ R.

Justify your answer in each case.

A.9. Given, R={(a, b): a, b  $\in$ N and a = b²}

(i)Let a = 2  $\in$ N

Then b = 2² = 4 $\in$ N

but a ≠ b.

Hence the given statement is not true.

(ii)For a=b² the inverse b=a² may not hold true

Example (4,2)  $\in$ R, a=4, b=2 and a=b²

but (2,4)  $\notin$ R.

Hence, the given statement is not true.

(iii)If (a,b)  $\in$ R

a=b²……(1)

and (b, c)  $\in$ R

b=c²…….(2)

so for (1) and (2),

a=(c²)²=c⁴.

is, a ≠c²,

Hence, (a, c)  $\notin$ R.

⸫The given statement is false.

Q10. Let A ={1,2,3,4}, B = {1,5,9,11,15,16} and f = {(1,5), (2,9), (3,1), (4,5), (2,11)} Are the following true?

(i) f is a relation from A to B (ii) f is a function from A to B.

Justify your answer in each case.

A.10. Given,

A={1,2,3,4}

B={1,5,9,11,15,16}

f={(1,5),(2,9),(3,1),(4,5),(2,11)}.

(i)As every element of f is an element of A × B

We can clearly say that f  $\subset$ A × B.

⸫f is a relation from A to B.

(ii)As the element 2 of the domain has two image i.e., 9 and 11. f is not a function.

Q11. Let f be the subset of Z × Z defined by f = {(ab, a + b) : a, b _ Z}. Is f a function from Z to Z? Justify your answer.

A.11. Given, f={(ab, a+b): a, b $\in$ z}

Let a=1 and b=1;                   a, b $\in$ z.

So, ab=1 × 1=1

a+b=1+1=2.

So, we have the order pair (1,2).

Now, let a= –1 and b= –1; a, b  $\in$ z

So, ab=(–1) × (–1)=1

a+b=(–1)+(–1)= –2

So, the ordered pair is (1, –2).

⸫The element 1 has two image i.e., 2 and –2.

Hence, f is not a function.

Q.12. Let A = {9,10,11,12,13} and let f : A→N be defined by f (n) = the highest prime factor of n. Find the range of f.

A.12. Given, A={9,10,11,12,13}.

f(x)=the highest prime factor of n.

and f: A → N.

Then, f(9)=3 [⸪ prime factor of 9=3]

f (10)=5 [⸪ prime factor of 10=2,5]

f(11)=11 [⸪ prime factor of 11 = 11]

f(12)=3 [⸪ prime factor of 12 = 2, 3]

f(13)=13 [⸪ prime factor of 13 = 13]

⸫Range of f=set of all image of f(x) = {3,5,11,13}.