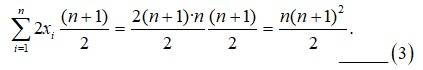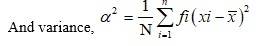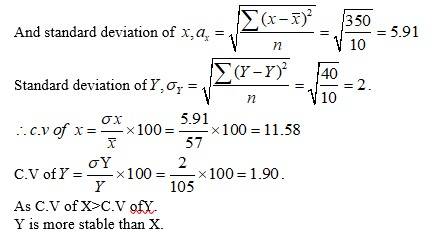NCERT Solutions Class 11 Maths Chapter 13 Statistics: Overview, Questions, Rules, Preparation

Ex.15.1

Q1. Find the mean deviation about the mean for the data in Exercises 1 and 2.

4, 7, 8, 9, 10, 12, 13, 17

A.1. Mean of the given observation is.

$\bar{x}=\frac{4+7+8+9+10+12+13+17}{8}$

$=\frac{80}{8}=10.$

Deviation of the respective observation about the mean  $\bar{x}$ i.e.,  $x_i-\bar{x}$ are 4–10,7–10,8–10,9–10,10–10,12–10,13–10,17–10

=6,-3,-2,-1,0,2,3,7

The absolute value of the deviation i.e.,  $\left|x_i-\bar{x}\right|$ are 6,3,2,1,0,2,3,7.

Therefore, the required mean deviation about the mean is

$\mathrm{M.D}=(\bar{x})=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|x_i-\bar{x}\right|}=\frac{6+3+2+1+0+2+3+7}{8}$

$=\frac{24}{8}$

= 3.

 

Q2. 38, 70, 48, 40, 42, 55, 63, 46, 54, 44

A.2. Mean of the given observation is.

$\bar{x}=\frac{38+70+48+40+42+55+63+46+54+44}{10}$

$=\frac{500}{10}=50.$

So,

xi	38	10	48	40	42	55	63	46	54	44
	12	20	2	10	8	5	13	4	4	6

Therefore, the required mean deviation about the mean is

$\text{\hspace{0.17em}M.D.}(\bar{x})=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|x_i-\bar{x}\right|}$

$=\frac{12+20+2+10+8+5+13+4+4+6}{10}$

$=\frac{84}{10}$

= 8.4

 

Q3. Find the mean deviation about the median for the data in Exercises 3 and 4.

13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17

A.3. Arranging the data in ascending order we get,

10,11,1112,13,13,14,16,16,17,17,18

As n=12, even

So, median is the mean of  ${(\frac{M}{2})th}^{}$ and  ${(\frac{M}{2}+1)th}^{}$ observation.

$\Rightarrow =\frac{{\mathrm{6thobservation}}^{}+{\mathrm{7thobservation}}^{}}{2}$

$M=\frac{13+14}{2}=\frac{27}{2}=13.5.$

So, deviation of respective observation about the median.  $M,\left|x_i-M\right|$ are

xi	10	11	11	12	13	13	14	16	16	17	17	18
	3.5	2.5	2.5	1.5	0.5	0.5	0.5	2.5	2.5	3.5	3.5	4.5

Therefore the mean deviation about the mean is

$\text{\hspace{0.17em}M.D.}(M)=\frac{1}{n}\times {\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|x_i-M\right|}$

$=\frac{1}{12}\times (3.5+2.5+2.5+1.5+0.5+0.5+0.5+2.5+2.5+3.5+3.5+4.5)$

$=\frac{28}{12}=2.33.$

 

Q4. 36, 72, 46, 42, 60, 45, 53, 46, 51, 49

A.4. Arranging the given data in ascending order we get,

36,42,45,46,46,49,51,53,60,72

As n = 10 (even)

$=\frac{\left(\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\text{\hspace{0.17em}thObservation}}^{}+{(\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+1)thObservation}^{}}{2}$

$\Rightarrow =\frac{{\mathrm{5thobservation}}^{}+{\mathrm{6thobservation}}^{}}{2}$

$=\frac{46+49}{2}$

$=\frac{95}{2}$

= 47.5

	36	42	45	46	46	49	51	53	60	72
	11.5	5.5	2.5	1.5	1.5	1.5	3.5	5.5	12.5	24.5

$\therefore$ M.D. (M)  $=\frac{1}{n}\times {\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|x_i-M\right|}$

$=\frac{1}{10}\times \left(11.5+5.5+2.5+1.5+1.5+1.5+3.5+5.5+12.5+24.5\right)$

$=\frac{70}{10}=7.$

 

Q5. Find the mean deviation about the mean for the data in Exercises 5 and 6.

 

$\begin{array}{c}=\frac{1}{29}\times 148\\ \end{array}$

= 5. 10

 

 

Ex.15.2

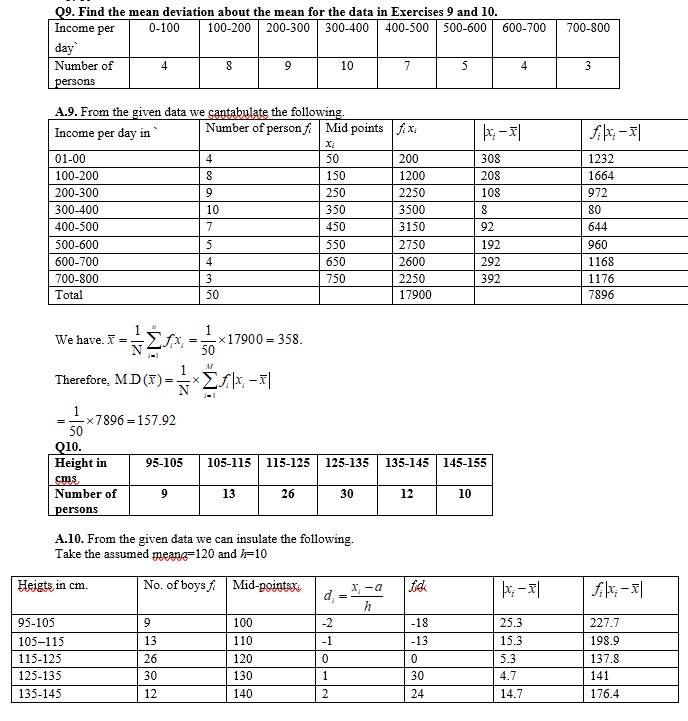
Q1. Find the mean and variance for each of the data in Exercies 1 to 5.

6, 7, 10, 12, 13, 4, 8, 12

A.1. The given data can be tabulated as.

 

we have,

mean,  $\bar{x}=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}}{n}=\frac{6+7+10+12+13+4+8+12}{8}=\frac{72}{8}=9.$

So, variance,  $\begin{array}{c}{a}^2=\frac{1}{8}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(x_i-\bar{x}\right)}^2}\\ \end{array}$

$=\frac{1}{8}\times 74=9.25$

 

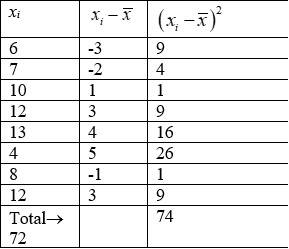
Q2. First n natural numbers

A.2. We know that,

Sum of first'n ' natural no  $=\frac{n(n+1)}{2}$

So, mean,  $\begin{array}{c}\bar{x}=\frac{\text{\hspace{0.17em}sumoffirst}\left(n\right)\text{\hspace{0.17em}naturalno}.=}{}\frac{n(n\text{\hspace{0.17em}+1})/2}{n}\\ no\; of\; observations\end{array}$

$=\frac{n+1}{2}$

So, Variance,  $a^2=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(x_i-\bar{x}\right)}^2}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(x_i-\left(\frac{n+1}{2}\right)\right)}^2}$

$\begin{array}{l}{a}^2=\frac{1}{n}\left[{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i^2}-{\displaystyle \underset{i=1}{\overset{n}{\sum }}2}{x}_i\left(\frac{n+1}{2}\right)+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(\frac{n+1}{2}\right)}^2}\right]\\ \_\_\_\_\_\_\_(1)\end{array}$

So,  $\begin{array}{c}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i^2}={(1)}^2+{(2)}^2+{(3)}^2+\dots +{(n)}^2\\ =\frac{n(n+1)(2n+1)}{6}\_\_\_\_\_\left(2\right).\end{array}$

 

And  ${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(\frac{n+1}{2}\right)}^2}=\frac{{(n+1)}^2}{4}{\displaystyle \underset{i=1}{\overset{n}{\sum }}1}.=\frac{n{(n+1)}^2}{4\cdot }\_\_\_\_\left(4\right).$

Putting (2), (3) and (4) in (1) we get,

$\begin{array}{c}{a}^2=\frac{1}{n}\left[\frac{n(n+1)(2n+1)}{6}-\frac{n{(n+1)}^2}{2}+\frac{n{(n+1)}^2}{4}\right]\\ \end{array}$

$\begin{array}{c}=\frac{(n+1)(2n+1)}{6}-\frac{{(n+1)}^2}{2}+\frac{{(n+1)}^2}{4}\\ \end{array}$

$\begin{array}{c}=\frac{(n+1)(2n+1)}{6}-\frac{{(n+1)}^2}{4}.\\ \end{array}$

$\begin{array}{c}=(n+1)\left[\frac{2n+1}{6}-\frac{(n+1)}{4}\right]\\ \end{array}$

$=(n+1)\left[\frac{4n+2-3n-3}{12}\right]$

$=\frac{(n+1)(n-1)}{12}=\frac{n^2-1}{12}.$

 

Q3. First 10 multiples of 3A.3. We have, first 10 multiples of 3=3,6,9,12,15,18,21,24,27,30.

So,  $\bar{x}=\frac{3+6+9+12+15+18+21+24+27+30}{10}=\frac{165}{10}=16.5$

We can now tabulate the given data as following.

Total

742.25

Therefore, variance,  $a^2=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(x_i-\bar{x}\right)}^2}$

$\begin{array}{c}=\frac{1}{10}\times 742.5\\ \end{array}$

= 74.25.

 

Q4.

xi	6	10	14	18	24	28	30
fi	2	4	7	12	8	4	3

 

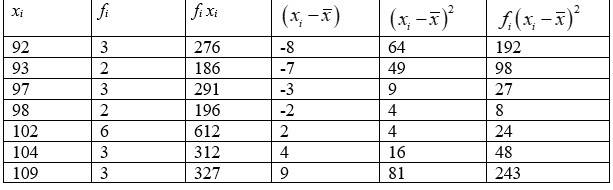
Q5.

xi	92	93	97	98	102	104	109
fi	3	2	3	2	6	3	3

A.5. The given data can be tabulated as follow

 

 

 

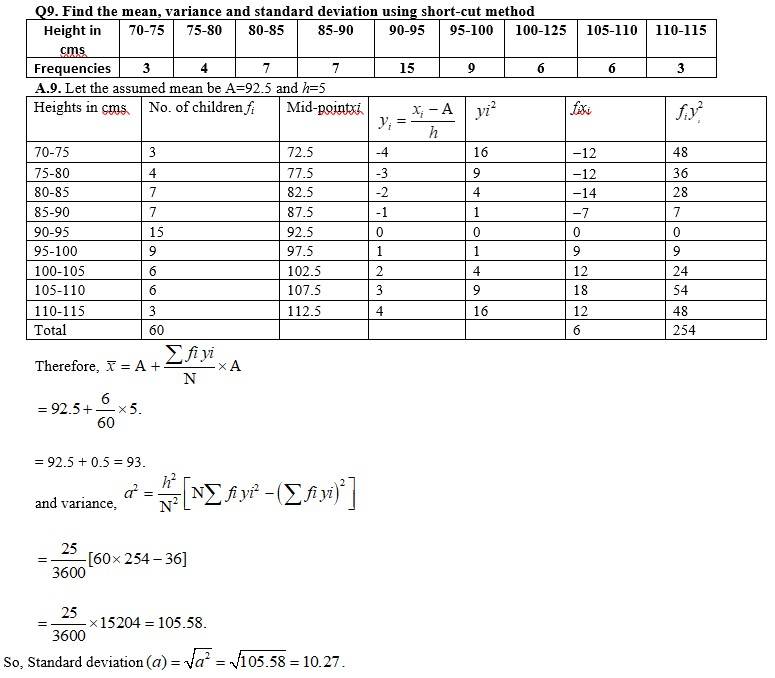
Q6.Find the mean and standard deviation using short-cut method.

xi	60	61	62	63	64	65	66	67	68
fi	2	1	12	29	25	12	10	4	5

 

 

Q7. Find the mean and variance for the following frequency distributions in Exercises7 and 8.

Classes	0-30	30-60	60-90	90-120	120-150	150-180	180-210
Frequencies	2	3	5	10	3	5	2

 

 

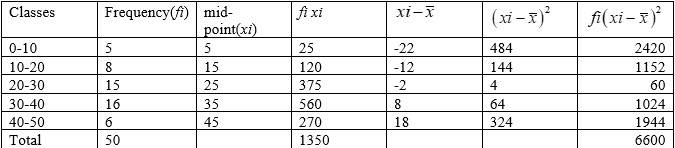
Q8.

Classes	0-10	10-20	20-30	30-40	40-50
Frequencies	5	8	15	16	6

A.8.

 

We have,  $N={\displaystyle \underset{i=1}{\overset{n}{\sum }}fi}=50$ .

So, mean,  $\bar{x}=\frac{1}{N}\times {\displaystyle \underset{i=1}{\overset{n}{\sum }}fi}xi=\frac{1350}{5}=27.$

$\begin{array}{c}\end{array}$

$\begin{array}{c}=\frac{1}{50}\times 6600\\ \end{array}$

= 132.

 

Q10. The diameters of circles (in mm) drawn in a design are given below:

Diameters	33-36	37-40	41-44	45-48	49-52
No. of circles	15	17	21	22	25

Calculate the standard deviation and mean diameter of the circles.

[ Hint First make the data continuous by making the classes as 32.5-36.5, 36.5-40.5,

40.5-44.5, 44.5 - 48.5, 48.5 - 52.5 and then proceed.]

A.10. The given data is converted into continuous frequency duration by subtracting and adding 0.5 from lower and upper limit respectively. Lit the assumed mean be A=42.5 and h=4

 

Ex. 15.3

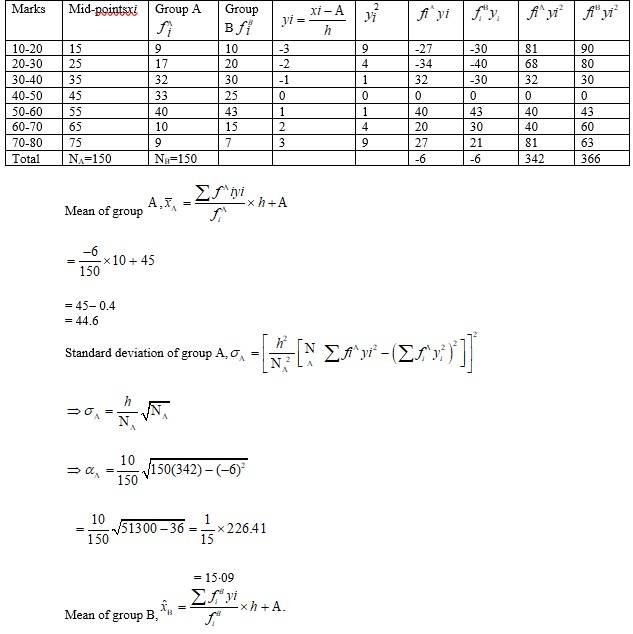
Q1. From the data given below state which group is more variable, A or B?

Marks	10-20	20-30	30-40	40-50	50-60	60-70	70-80
Group A	9	17	32	33	40	10	9
Group B	10	20	30	25	43	15	7

A.1. Let the assumed mean be A=45 and h=10. Then we can tabulate the given data as following.

 

$\begin{array}{c}=\frac{-6}{150}\times 10+45.\\ \end{array}$

= 44.6

 

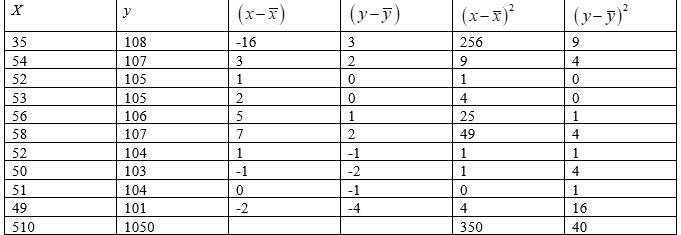
Q2. From the prices of shares X and Y below, find out which is more stable in value:

X	35	54	52	53	56	58	52	50	51	49
Y	108	107	105	105	106	107	104	103	104	101

A.2. We can tabulate the given data as follows.

 

Total =

Mean of  $x,\bar{x}=\frac{{\displaystyle \underset{}{\overset{}{\sum }}xi}}{n}=\frac{510}{10}=51.$

Mean of  $Y,\bar{Y}=\frac{{\displaystyle \underset{}{\overset{}{\sum }}Yi}}{n}=\frac{1050}{10}=105$ .

 

 

 

Q4. The following is the record of goals scored by team A in a football session:

No. of goals scored

0

1

2

3

4

No. of matches

1

9

7

5

3

For the team B, mean number of goals scored per match was 2 with a standard

deviation 1.25 goals. Find which team may be considered more consistent?

 

 

Q5. The sum and sum of squares corresponding to length x (in cm) and weight y

(ingm) of 50 plant products are given below:

${\displaystyle \underset{i=1}{\overset{50}{\sum }}=x_i=212,}{\displaystyle \underset{i=1}{\overset{50}{\sum }}{x}_i^2=902.8,{\displaystyle \underset{i=1}{\overset{50}{\sum }}{y}_i=261,}}{\displaystyle \underset{i=1}{\overset{50}{\sum }}{y_i}^2=1457.6}$

Which is more varying, the length or weight?

A.5. Give, n=50.

$\begin{array}{l}\\ {\displaystyle \underset{i=1}{\overset{n}{\sum }}xi}=212{\displaystyle \underset{i=1}{\overset{50}{\sum }}x{i}^2}=902.8\\ \end{array}$

${\displaystyle \underset{i=1}{\overset{50}{\sum }}yi}=261{\displaystyle \underset{i=1}{\overset{50}{\sum }}y{i}^2}=1457.6$

So,  $\bar{x}=\frac{{\displaystyle \underset{i=1}{\overset{50}{\sum }}{x}_i}}{n}=\frac{212}{50}=4.24$

 

Miscellaneous Example

Q1. The mean and variance of eight observations are 9 and 9.25, respectively. If six of the observations are 6, 7, 10, 12, 12 and 13, find the remaining two observations.

A.1. Let the other two observation be x and y.

Therefore, the series is 6, 7, 10, 12, 12, 13, x, y.

So, Mean  $\bar{x}=9$

$\Rightarrow \frac{6+7+10+12+12+13+x+y}{8}=9$

$\Rightarrow x+y=72-60$

$\Rightarrow x+y=12$ ….. (1)

And, variance = 9.25

$\Rightarrow \frac{1}{8}{\displaystyle \underset{i=1}{\overset{8}{\sum }}{\left(x_i-\bar{x}\right)}^2=9.25}$

$\Rightarrow {\left(-3\right)}^2+{\left(-2\right)}^2+{\left(1\right)}^2+{\left(3\right)}^2+{\left(3\right)}^2+{\left(4\right)}^2+{\left(x-9\right)}^2+{\left(y-9\right)}^2=9.25\times 8$

$\Rightarrow$ 9 + 4 + 1 + 9 + 9 + 16 + x2 + 81 - 18x + y2 + 81 - 18y = 74

$\Rightarrow 210+x^2+y^2-18\left(x+y\right)=74$

$\Rightarrow x^2+y^2=74-210+18\left(12\right)$ [  $\therefore$ equation (1)]

$\Rightarrow x^2+y^2=80$ ……(2)

Squaring Equation (1) we get,

$x^2+y^2+2xy=144$

$\Rightarrow 80+2xy=144$

$\Rightarrow 2xy=64$ (3)

Subtracting (3) from (2) we get,

$x^2+y^2-2xy=16$

$\Rightarrow {\left(x-y\right)}^2=4^2$

$\Rightarrow x-y=\pm 4$ ……(4)

From (1) and (4)

Case I, x + y =12 and x - y = 4

$\Rightarrow$ x = 8  and y = 4

Case II,x + y =12    and  x – y = -4

$\Rightarrow$ x = 4  and y = 8.

Hence, the remaining observations are 8 and 4.

 

Q2. The mean and variance of 7 observations are 8 and 16, respectively. If five of the observations are 2, 4, 10, 12, 14. Find the remaining two observations.

A.2. Let the other two observation be x and y. Then, the series is 2, 4, 10, 12, 14, x, y.

So, mean,  $\bar{x}=\frac{2+4+10+12+14+x+y}{7}=8.$

$\Rightarrow 8\times 7=42+x+y.$

$\Rightarrow x+y=14$ ….(1)

And variance =  $\frac{1}{n}{\displaystyle \underset{i=1}{\overset{7}{\sum }}{\left(x_i-\bar{x}\right)}^2}$

$\Rightarrow 16=\frac{1}{7}\left[{\left(-6\right)}^2+{\left(-4\right)}^2+{\left(-2\right)}^2+{\left(4\right)}^2+{\left(6\right)}^2+{\left(x-8\right)}^2+{\left(y-8\right)}^2\right]$

$\Rightarrow 36+16+4+36+x^{2}64-16x+y^2+64-16y=112.$

$\Rightarrow 236+x^2{y}^2-16\left(x+y\right)=112$

$\Rightarrow x^2+y^2=112-236+16\left(14\right)\left[\left(1\right)\right]$

$\Rightarrow x^2+y^2=100$ ….(2)

Squaring eqn (1) we get,

$x^2+y^2+2xy=196$

$\Rightarrow 2xy=96-100$

$\Rightarrow 2xy=96$ …..(3)

Subtracting eqn (3) from (2) we get,

$x^2+y^2-2xy=4$

$\Rightarrow {\left(x-y\right)}^2=2^2$

$\Rightarrow x-y=\pm 2.$ ….(4)

Using eqn (1) and (2) we get,

Case I. x + y = 14 and x – y = 2

$\Rightarrow$ x = 8 and y = 6

Case II. x + y = 14 and x – y = -2

$\Rightarrow$ x = 6 and y = 8

Hence, the remaining observations are 6 and 8.

 

Q3. The mean and standard deviation of six observations are 8 and 4, respectively. If each observation is multiplied by 3, find the new mean and new standard deviation of the resulting observations.

A.3. Let ‘x’ be the given observations with n = 6.

 

 

Q4. Given that  $\bar{x}$ is the mean and σ2 is the variance of n observations x₁, x₂, ...,xn. Prove that the mean and variance of the observations ax₁, ax₂, ax₃, ...., ax_n are a $\bar{x}$ and a₂ σ₂, respectively, (a ≠ 0).

A.4. For n observations x₁, x₂,……., x_n .

We have mean =  $\bar{x}=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}}{n}\left(1\right)$

and variance =  ${\sigma }^2=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(x_i-\bar{x}\right)}^2\left(2\right)}$

Let y_i  be the new observations with same n.

So,  y_i = ax_i      (3)

Now mean,  $\bar{y}=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{y}_i}}{n}=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}a{x}_i}}{n}=\frac{a{\displaystyle \underset{i=1}{\overset{n}{\sum }}{y}_i}}{n}=a\bar{x}\left[\left(1\right)\right]$

So   $\bar{y}=a\bar{x}\left(4\right)$

And, putting (3) and (4) in (2) we get,

${\sigma }^2=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(\frac{y_i}{a}-\frac{\bar{y}}{a}\right)}^2}$

$\Rightarrow {\sigma }^2=\frac{1}{a^2}\left[\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-\bar{y}\right)}^2}\right]$

$\Rightarrow {\left({\sigma }^{\text{'}}\right)}^2={\sigma }^2{\alpha }^2.$

Hence, the mean and variance of ax₁, ax₂, ……, ax_n  are $a\bar{x}$ and a² σ² .

 

Q5. The mean and standard deviation of 20 observations are found to be 10 and 2, respectively. On rechecking, it was found that an observation 8 was incorrect. Calculate the correct mean and standard deviation in each of the following cases:

(i) If wrong item is omitted. (ii) If it is replaced by 12.

A.5. (i) Given, n = 20.

Incorrect mean  $(\bar{x})=10$

Incorrect standard deviation  $(\sigma )=2$

We know that,

$\bar{x}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}$

$\Rightarrow 10=\frac{1}{20}{\displaystyle \underset{i=1}{\overset{20}{\sum }}{x}_i}$

$\Rightarrow {\displaystyle \underset{i=1}{\overset{20}{\sum }}{x}_i}=200$

So, incorrect sum of observation = 200.

correct sum of observation =200 – 8 = 192

And correct mean  $=\frac{192}{19}=10.1$

 

 

Q6. The mean and standard deviation of marks obtained by 50 students of a class in three subjects, Mathematics, Physics and Chemistry are given below:

Subject                                                        Mathematics           Physics                Chemistry

Mean                                                             42                            32                         40.9

Standard                                                       12                           15                          20

deviation

Which of the three subjects shows the highest variability in marks and which

shows the lowest?

A.6. C.V in mathematics =  $\frac{12}{42}\times 100=28.57.$

C.V in Physics =  $\frac{15}{32}\times 100=46.87.$

C.V in chemistry =  $\frac{20}{40.9}\times 100=48.89$

$\therefore$  Chemistry has highest variability and mathematics has lowest variability.

 

Q7. The mean and standard deviation of a group of 100 observations were found to be 20 and 3, respectively. Later on it was found that three observations were incorrect, which were recorded as 21, 21 and 18. Find the mean and standard deviation if the incorrect observations are omitted.

A.7. Given, n = 100.

incorrect mean (  $\bar{x}$ ) = 20.

incorrect standard deviation (σ) = 3

We know that,

$\bar{x}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{n}_i}$

$\Rightarrow 20=\frac{1}{100}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{n}_i}$

$\Rightarrow {\displaystyle \underset{i=1}{\overset{n}{\sum }}{n}_i}=2000.$

So, incorrect sum of observation = 2000

Correct sum of observation  $=2000-21-21-18$

= 1940