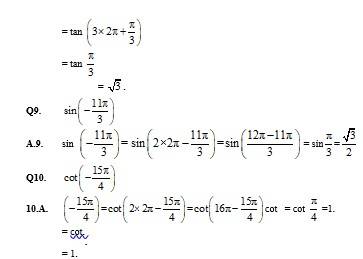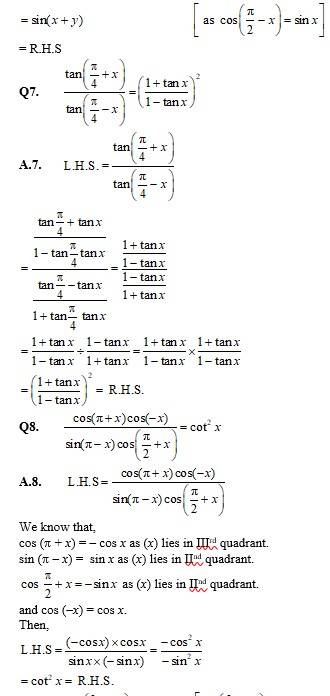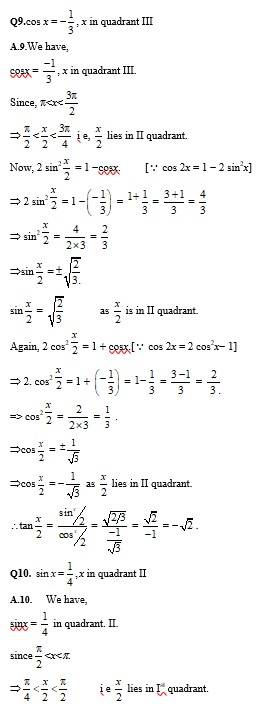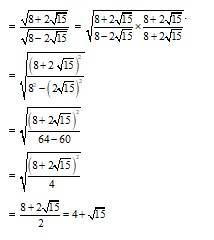NCERT Solutions Class 11 Maths Chapter 3 Trigonometric Functions: Topics, Questions, Easy Tricks & Preparation

• Angles
• Trigonometric functions
• Trigonometric Functions of Sum and Difference of Two Angles 
• Trigonometric Equations

Check the NCERT Solutions Maths Class 11 Chapter 3 Trigonometric Functions below.

Q 3.1 Find the radian measures corresponding to the following degree measures:

(i)         25°      

(ii)        – 47°30'        

(iii)       240°    

(iv)       520°

A 3.1

(i)            25°

Solution:We know that 180° = π radian.

Hence, 25° = π/180 X 25 radian= 5π/36 radians.

(ii).-47°30'

Solution: We know that 180°=π radian,

Hence, -47°30' = -47 × 1/2 degree= -47/2× π/180 radians.

= -19π/72 radians

(iii) 240°

Solution:We know that, 180°=π radian.

Hence, 240°= 240× π/180 radian.

= 4π/3 radian.

(iv) 520°

Solution: We know that, 180°= π radian.

Hence, 520°= 520°× π/180 radian.

= 26π/9 radian.

Q 3.3 A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

A 3.3 Given that a wheel makes 360 revolutions in one minute

Then, number of revolutions in one second = 360/60 =6.

In 1 complete revolution the wheel turns 360°= 2 π radian.

So, In 6 revolution, the wheel will turns 6×2π radian = 12π radian.

Hence, in one second the wheel will turn an angle of 12π radian.

Q Find the values of the trigonometric functions in sin 765°

A 3.2.6

sin 765°

We know that value of sun x repeats after an interval of 2π or 360°.

Sin (765°) = sin (2×360°+45°)

= sin 45°

= 1/√2

Download Here NCERT Class 11th Maths Chapter 3 Trigonometric Functions

Exercise 3.1

Q1. Find the radian measures corresponding to the following degree measures:

(i) 25° (ii) – 47°30′ (iii) 240° (iv) 520°

A.1. (i)25°

Solution:We know that 180° = π radian.

Hence, 25° =  $\frac{\pi }{180}$ 25 radian=  $\frac{\mathrm{5\pi }}{36}$ radians.

(ii).47°30′

Solution: We know that 180° = π radian,

Hence, -47°30′= -47 × $\frac{1}{2}$ degree=  $\frac{-47}{2}$ × $\frac{\pi }{\mathrm{180°}}$ radians.

=  $-\frac{1\mathrm{9\pi }}{72}$ radians

(iii) 240°

Solution:We know that, 180°= radian.

Hence, 240°= 240× $\frac{\pi }{\mathrm{180 }}$ radian.

=  $\frac{\mathrm{4\pi }}{3}$ radian.

(iv) 520°

Solution: We know that, 180= radian.

Hence, 520°= 520°× $\frac{\pi }{\mathrm{180 }}$radian.

=  $\frac{2\mathrm{6\pi }}{9}$ radian.

 

Q2. Find the degree measures corresponding to the following radian measures  $\left(Use\pi =\frac{22}{7}\right).$

(i) $\frac{11}{16}$ (ii)-4 (iii) $\frac{5\pi }{3}$ (iv)  $\frac{7\pi }{6}$

A.2. (i)  $\frac{11}{16}$

We know that radian= 180°,

Hence,  $\frac{11}{16}$ radian=  $\frac{11}{16}$ × $\frac{\mathrm{<br>}\mathrm{180°}}{\mathrm{\pi }}$ =  $\frac{11}{16}$ ×  $\frac{180°}{22/7}$ =  $\frac{11}{16}$ ×  $\frac{7}{22}$ ×180 $\frac{°}{}$

=  ${\left(\frac{315}{8}\right)}^0$

=39 0  $\frac{3°}{8}$

= 39 $\frac{°}{}$+  $\frac{3\times 60}{8}$ minute (as 1 $\frac{°}{}$=60′)

=39°+22′+  ${\left(\frac{1}{2}\right)}^{\text{'}}$

=39°+22′+  ${\left(\frac{60}{2}\right)}^{\text{'}\text{'}}$ (as 1′=60”)

=39°+22′+30”.

=39° 22′ 30”.

(ii) -4

We know that radian = 180°.

Hence: -4 radian = -4× ${\left(\frac{\mathrm{180°}}{\mathrm{\pi }}\right)}^{}$ = 4×  $\frac{180°}{\raisebox{1ex}{$22$}\!\left/ \!\raisebox{-1ex}{$7$}\right.}$ = 4×180°×  $\frac{7}{22}$ .

= -  ${\left(\frac{2520}{11}\right)}^0$

=229 0  $\frac{1°}{11}$

=229+  $\frac{1\times 60\text{'}}{11}$

=229+5′+  ${\left(\frac{5}{11}\right)}^{\text{'}}$ .

=229°+5′+27″

=229° 5′27″

(iii)  $\frac{\mathrm{5\pi }}{3}.$ .

Solution: We know that, π radian= 180°.

Here  $\frac{\mathrm{5\pi }}{3}$ radian =  $\frac{\mathrm{5\pi }}{3}$ × $\frac{\mathrm{180°}}{\mathrm{\pi }}$ $\frac{\mathrm{<br>}}{}$ =300°

(iv)  $\frac{\mathrm{7\pi }}{6}$

Solution: We know that radian =180° .

Here,  $\frac{\mathrm{7\pi }}{6}$ radian =  $\frac{\mathrm{7\pi }}{6}$ × $\frac{\mathrm{180°}}{\mathrm{\pi }}$=210°

 

Q3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

A.3. Given that a wheel makes 360 revolutions in one minute

Then, number of revolutions in one second =  $\frac{360}{60}$ =6.

In 1 complete revolution the wheel turns 360°= 2π radian.

So, In 6 revolution, the wheel will turns 6×2π radian = 12π radian.

Hence, in one second the wheel will turn an angle of 12π radian.

 

Q4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm $\left(Use\pi =\frac{22}{7}\right).$

A.4. Here l = 22cm.

r =100cm.

Ø = ?

Hence by r = $\frac{\mathrm{<br>}1}{\mathrm{Ø}}$

= Ø = $\frac{l}{r}$ =  $\frac{22}{100}$ radian

=  $\frac{22}{100}$ × $\frac{\mathrm{180°}}{\mathrm{<br>}\mathrm{\pi }}$ $\frac{}{}$

=  $\frac{22}{100}$ × 180° ×  $\frac{7}{22}$

=  ${\left(\frac{63}{5}\right)}^0$

=12  $\frac{3°}{5}$ = 12°  $\frac{3\times 60\text{'}}{5}=12°36\text{'}$

 

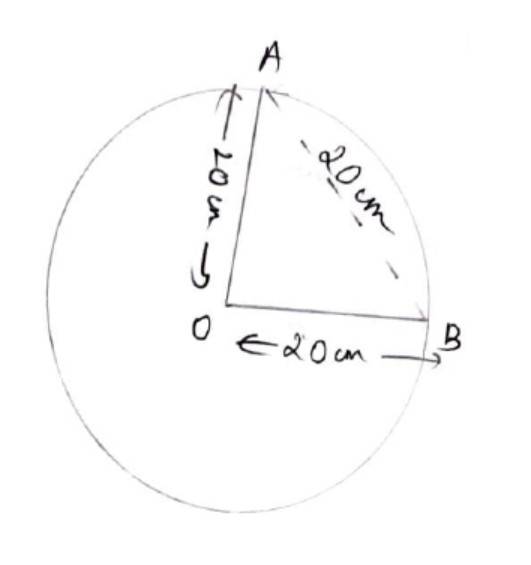
Q5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.

So, radius, r =  $\frac{40}{2}$ cm = 20 cm

Length of chord (AB) = 20cm

In OAB

OA = OB=AB=20 cm

Hence, AOAB is equilateral triangle and end of the angle is 60°

:. Ø =60° = 60 × $\frac{\mathrm{<br>}\mathrm{\pi }}{180}$ radian = $\frac{\mathrm{\pi }}{3}$ radian

Hence, length of minor are of the chord, l=rØ.

l = 20 × $\frac{\mathrm{\pi }}{3}$ cm

l =  $\frac{2\mathrm{0\pi }}{3}$ cm.

 

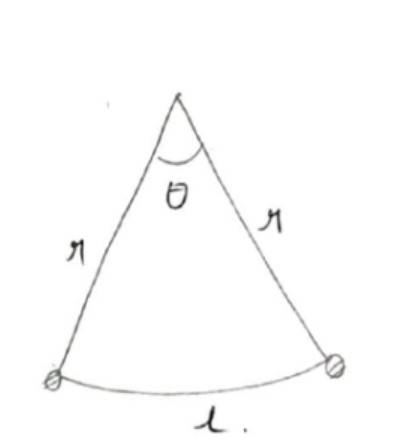
Q7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length

(i) 10 cm (ii) 15 cm (iii) 21 cm

A.7. Here,

r= length of pendulum.

r= 75 cm.

(i)Are of length, l = 10 cm

Ø=  $\frac{l}{r}$ =  $\frac{10cm}{75cm}=\frac{2}{15}$ radian.

(ii) are of length, l = 15 cm.

So, Ø=  $\frac{l}{r}$ =  $\frac{15cm}{75cm}=\frac{1}{5}$ radian.

(iii) are for length, l= 21 cm.

So, Ø=  $\frac{l}{r}=\frac{21cm}{75cm}=\frac{7}{25}$ radian.

 

Exercise 3.2

Find the values of other five trigonometric functions in Exercises 1 to 5.

 

Exercise 13.3

Q1.  $si{n}^2\frac{\pi }{6}+co{s}^2\frac{\pi }{3}-ta{n}^2\frac{\pi }{4}=-\frac{1}{2}$

A.1.

$\begin{array}{l}{\left(\frac{1}{2}\right)}^2+{\left(\frac{1}{2}\right)}^2-1^2\\ =\frac{1}{4}+\frac{1}{4}-1\\ =\frac{1+1+4}{4}\\ =\frac{-2}{4}\\ =\frac{-1}{2}\end{array}$

=R.H.S

 

Q2.  $2Si{n}^2\frac{\pi }{6}+cose{c}^2\frac{7\pi }{6}co{s}^2\frac{\pi }{3}=\frac{3}{2}$

$=\frac{1}{2}+4.\frac{1}{4}$

$=\frac{1}{2}+1$  $=\frac{3}{2}$

= R.H.S.

 

Q5. Find the value of:

(i) sin 75° (ii) tan 15°

A.5. (i) sin 75°= sin (45°+30°)

Using sin (x + y)= sin x cos y + cos x sin y we can write

sin 75°

 

Q9.  $cos\left(\frac{3\pi }{2}+x\right)cos\left(2\pi +x\right)\left[cot\left(\frac{3\pi }{2}-x\right)+cot\left(2\pi +x\right)\right]=1$

A.9.  $=cos\left(\frac{3\pi }{2}+x\right)cos(2\pi +x)\left[cot\left(\frac{3\pi }{2}-x\right)+cot(2\pi +x)\right]$

Here,

$cos\left(\frac{3\pi }{2}+x\right)=cos\left(\frac{4\pi -\pi }{2}+x\right)=cos\left(2\pi -\frac{\pi }{2}+x\right)$

$=cos\left[2\pi -\left(\frac{\pi }{2}-x\right)\right];VI\; quadrant$

$cos\left(\frac{\pi }{2}-x\right);Ist\; quadrant\mathrm{<br>}{}^{}$

$=sinx$

$cos(2x+x)=cosx,x{}^{}\text{\hspace{0.17em}lies in Ist quadrant}$

$cot(2\pi +x)=cotx;x\text{\hspace{0.17em}lies in Ist quadrant}{}^{}\text{<br>}$

$cot\left(\frac{3\pi }{2}-x\right)=cot\left[\frac{4\pi -\pi }{2}-x\right]$

$=cot\left[2\pi -\frac{\pi }{2}-x\right]$

$=cot\left[2x-\left(\frac{\pi }{2}+x\right)\right];\; VIth\; quadrant{}^{}$

$=-cot\left(\frac{\pi }{2}+x\right);IIndquadrant{}^{}$

$=-(-tanx)$

$=tanx.$

So.  $=sinxcosx[tanx+cotx]$

$=sinxcosx\left[\frac{sinx}{cosx}+\frac{cosx}{sinx}\right]$

$=sinxcosx\frac{\left(si{n}^{2}x+co{s}^{2}x\right)}{cosxsinx}$

$=si{n}^{2}x+co{s}^{2}x$

= 1

= R.H.S.

 

Q10. sin (n + 1)xsin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x

A.10.  $=sin(x+1)xsin(x+2)x+cos(x+1)xcos(x+2)x.$

$=cos(x+1)xcos(x+2)x+sin(x+1)xsin(x+2)x.$

Let A $=(n+1)\mathrm{x\; B}=(n+2)x.$

So, L.H.S= $co\mathrm{sA}co\mathrm{sB}+si\mathrm{nA}si\mathrm{nB}.$

$=cos(A-B)$

Putting values of A and B we get,

$\mathrm{L.H.S\; c}os[(n+1)x-(n+2)x]$

$=cos[nx+x-nx-2x]$

$=cos(-x)$

$=cosx=R.H.S$

 

Q11.  $cos\left(\frac{3\pi }{4}+x\right)-cos\left(\frac{3\pi }{4}-x\right)=-\surd 2sinx$

A.11. L.H.S $=cos\left(\frac{3\pi }{4}+x\right)-cos\left(\frac{3\pi }{4}-x\right)$

Using cos (A + B) = cos A cos B – sin A sin B

and cos (A – B) = cos A cos B + sin A sin B

$L.H.S=[cos\frac{3\pi }{4}cosx-sin\frac{3\pi }{4}sinx]-\left[cos\frac{3\pi }{4}cosx+sin\frac{3\pi }{4}sinx\right]$

$=cos\frac{3\pi }{4}cosx-sin\frac{3\pi }{4}sinx-cos\frac{3\pi }{4}cosx-sin\frac{3\pi }{4}sinx.$

$=-2sin\frac{3\pi }{4}sinx.$

$=-2sin\left(\frac{4\pi -\pi }{4}\right)sinx.$

$=-2sin\frac{\pi }{4}·sinx=-2\pi \frac{1}{}·sinx=-sinx=$

 

Q12. sin²6x – sin²4x = sin 2x sin 10x

A.12.  $=si{n}^{2}6x-si{n}^{2}4x.$

$=(sin6x+sin4x)(sin6x-sin4x).\left[a^2-b^2=(a-b)(a+b)\right]$

Using  $si\mathrm{nA}+si\mathrm{nB}=2sin\frac{A+B}{2}\frac{Sin\; A-B}{2}$

and  $si\mathrm{nA}-si\mathrm{nB}=2cos\frac{A+B}{2}sin\frac{A-B}{2}$

So,

$L.H.S\; =\left(2sin\left(\frac{6x+4x}{2}\right)cos\left(\frac{6x-4x}{2}\right)\right)\left(2cos\left(\frac{6x+4x}{2}\right)sin\left(\frac{6x-4x}{2}\right)\right)$

$=\left(2sin\frac{10x}{2}cos\frac{2x}{2}\right)\left(2cos\frac{10x}{2}sin\frac{2x}{2}\right)$

$=2sin5xcosx\cdot 2cos5xsinx$

$=2sin5xcos5x\cdot 2csinxcosx.$

As  $sin2\theta =2sin\theta cos\theta$ we can write.

$\mathrm{L.H.S\; =\; s}in\left(2\times 5x\right)=sin(2\times x)$

$=sin10xsin2x=R.H.S$

 

Q13. cos²2x – cos²6x = sin 4x sin 8x

A.13.  $=co{s}^{2}2x-co{s}^{2}6x$

$=(cos2x+cos6x)(cos2x-cos6x)\left[\because a^2-b^2=(a-b)(a+b)\right]$

Using  $co\mathrm{sA}+co\mathrm{sB}=2cos\frac{A+B}{2}\frac{CosA-B}{2}$

$co\mathrm{sA}-co\mathrm{sB}=-2sin\frac{A+B}{2}sin\frac{A-B}{2}$

$L.H.S=\left[2cos\left(\frac{2x+6x}{2}\right)cos\left(\frac{2x-6x}{2}\right)\right]\left[-2sin\frac{2x+6x}{2}sin\left(\frac{2x-6x}{2}\right)\right]$

$=\left[2cos\frac{8x}{2}cos\left(-\frac{4x}{2}\right)\right]\left[-2sin\left(\frac{8x}{2}\right)sin\left(-\frac{4x}{2}\right)\right]$

$=2cos4xcos2x\times 2sin4x·sin2x[\because cos(-x)=cosx;sin(-x)=-sinx]$

$=2sin4xcos4x\times 2sin2xcos2x$

As sin 2Ø = 2 sin ØcosØ.

L.H.S. = sin (2× 4x) sin(2× 2x)

= sin 8x sin 4x

= R.H.S.

 

Q14. sin2 x + 2 sin 4x + sin 6x = 4 cos²x sin 4x

A.14. L.H.S. = sin 2x + 2 sin 4x + sin 6x

Using sin A + sin B = 2 sin $\frac{A+B}{2}$ cos  $\frac{A-B}{2}$ we have,

L.H.S. = (sin 2x + sin 6x) + 2 sin 4x

$=2sin\left(\frac{2x+6x}{2}\right)cos\left(\frac{2x-6x}{2}\right)+2sin4x.$

$=2sin\frac{8x}{2}cos\left(-\frac{4x}{2}\right)+2sin4x.$

$=2sin4xcos2x+2sin4x[\because cos(-x)=x]$

$=2sin4x[cos2x+1]$

We know that,

$cos2x=2co{s}^{2}x-1$

$\Rightarrow cos2x+1=2co{s}^{2}x$

Hence,

$=2sin4x\left(2co{s}^{2}x\right)$

$=4co{s}^{2}xsin4x$

= R.H.S.

 

Q15. cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)

A.15.  $=cot4x(sin5x+sin3x)$

$=cot4x\left[2sin\left(\frac{5x+3x}{2}\right)cos\left(\frac{5x-3x}{2}\right)\right][\begin{array}{cc}\hfill \because sinA+sinB=\hfill & \hfill 2sin\frac{A+B}{2}cos\frac{A-B}{2}]\hfill \end{array}$

$=cot4x\left[2sin\frac{8x}{2}cos\frac{2x}{2}\right]$

$=\frac{cos4x}{4x}\times 2sin4xcosx$

$=2·cos4x·cosx$

$R.H.S=cotx[sin5x-sin3x]$

$=cotx\left[2·cos\left(\frac{5x+3x}{2}\right)sin\left(\frac{5x-3x}{2}\right)\right]\left[\begin{array}{cc}\hfill \because sinA-sinB=\hfill & \hfill 2cos\frac{A+B}{2}sin\frac{A-B}{2}\hfill \end{array}\right]$

$=cotx\left[2cos\frac{8x}{2}·sin\frac{2x}{2}\right]$

$=\frac{cosx}{sinx}·2cos4xsinx$

$=2·cos4x·cosx.$

Hence, L.H.S. = R.H.S.

 

Q16.  $\frac{cos9x-cos5x}{sin17x-sin3x}=-\frac{sin2x}{cos10x}$

A.16. L.H.S $=\frac{cos9x-cos5x}{sin17x-sin3x}$

$=\frac{-2sin\left(\frac{9x+5x}{2}\right)sin\left(\frac{9x-5x}{2}\right)}{2cos\left(\frac{17x+3x}{2}\right)sin\left(\frac{17x-3x}{2}\right)}$

$=\frac{-sin\frac{14x}{2}sin\frac{4x}{2}}{cos\frac{20x}{2}sin\frac{14x}{2}}=\frac{-sin7xsin2x}{cos10xsin7x}=\frac{-sin2x}{cos10x}$

= R.H.S

 

Q17.  $\frac{sin5x+sin3x}{cos5x+cos3x}=tan4x$

A.17. L.H.S $=\frac{sin5x+sin3x}{cos5x+cos3x.}$

$=\frac{2sin\left(\frac{5x+3x}{2}\right)cos\left(\frac{5x-3x}{2}\right)}{2cos\left(\frac{5x+3x}{2}\right)cos\left(\frac{5x-3x}{2}\right)}$

$=\frac{sin\frac{8x}{2}cos\frac{2x}{2}}{cos\frac{8x}{2}cos\frac{2x}{2}}$

$=\frac{sin4x}{cos4x}=tan4x=R.H.S$

 

Q18.  $\frac{sinx-siny}{cosx+cosy}=tan\frac{x-y}{2}$

A.18. L.H.S $=\frac{sinx-siny}{cosx+cosy}$

$=\frac{2cos\frac{x+y}{2}sin\frac{x-y}{2}}{2cos\frac{x+y}{2}cos\frac{x-y}{2}}$

$=\frac{sin\left(\frac{x-y}{2}\right)}{cos\left(\frac{x-y}{2}\right)}$

$=tan\left(\frac{x-y}{2}\right)\text{\hspace{0.17em}=R.H.S}$

 

Q19.  $\frac{sinx+sin3x}{cosx+cos3x}=tan2x$

A.19.  $=\frac{sinx+sin3x}{cosx+cos3x}$

$=\frac{2\left(\frac{x+3x}{2}\right)cos\left(\frac{x-3x}{2}\right)}{2cos\left(\frac{x+3x}{2}\right)cos\left(\frac{x-3x}{2}\right)}$

$=\frac{sin\frac{4x}{2}}{cos\frac{4x}{2}}$

$=\frac{sin2x}{cos2x}$

$=tan2x=R.H.S$

 

Q20.  $\frac{sinx-sin3x}{si{n}^{2}x-co{s}^{2}x}=2sinx$

A.20. L.H.S $=\frac{sinx-sin3x}{si{n}^{2}x-co{s}^{2}x}$

$=\frac{2cos\left(\frac{x+3x}{2}\right)sin\frac{x-3x}{2}}{-\left(co{s}^{2}x-si{n}^{2}x\right)}$

$=\frac{2cos\frac{4x}{2}sin\left(-\frac{2x}{2}\right)}{-cos2x}\left[\because cos2x=co{s}^{2}x-si{n}^{2}x\right]$

$=-\frac{2cos2xsinx}{-cos2x}[\because sin(-x)=-sinx]$

= 2 sin x

= R.H.S.

 

Q21.  $\frac{cos4x+cos3x+cos2x}{sin4x+sin3x+sin2x}=cot3x$

A.21. L.H.S $=\frac{cos4x+cos3x+cos2x}{sin4x+sin3x+sin2x.}$

$=\frac{(cos4x+cos2x)+cos3x}{(sin4x+sin2x)+sin3x}.$

$=\frac{2cos\left(\frac{4x+2x}{2}\right)cos\left(\frac{4x-2x}{2}\right)+cos3x}{2sin\left(\frac{4x+2x}{2}\right)cos\left(\frac{4x-2x}{2}\right)sin3x}.$

$=\frac{2cos\frac{6x}{2}cos\frac{2x}{2}+cos3x}{2sin\frac{6x}{2}cos\frac{2x}{2}+sin3x}$

$=\frac{2cos3xcosx+cos3x}{2sin3xcosx+3x}$

$=\frac{cos3x}{sin3x}\times \frac{(2cosx+1)}{(2cosx+1)}$

$=cot3x=R.H.S$

 

Q22. cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1

A.22. L.H.S. = cot x cot 2x – cot 2x cot 3x – cot 3x cot x.

= cot x cot 2x – cot 3x (cot 2x + cot x)

= cot x cot 2x – (cot 2x + cot x)[cot (2x + x)]

We know that,

$cot(A+B)=\frac{co\mathrm{tA}co\mathrm{tB}-1}{co\mathrm{tA}+co\mathrm{tB}}$ we can write

$L.H.S=cotxcot2x-(cot2x+cotx)\left[\frac{cot2x·cotx-1}{cot2x+cotx}\right]$

= cot x cot 2x – cot 2x cot x + 1

= 1

= R.H.S.

 

Q23.  $tan4x=\frac{4tanx\left(1-ta{n}^{2}x\right)}{1-6ta{n}^{2}x+ta{n}^{4}x}$

A.23. L.H.S. = tan 4x

We know that,

$tan2=\frac{2tan}{1-ta{n}^2}.$ , we can write

$L.H.S=tan2(2x)=\frac{2tan2x}{1-ta{n}^{2}2x.}$

$=\frac{2\left(\frac{2tanx}{1-ta{n}^{2}x}\right)}{1-{\left(\frac{2tanx}{1-ta{n}^{2}x}\right)}^2}$

$=\frac{\frac{4tanx}{\left(1-ta{n}^{2}x\right)}}{\frac{{\left(1-ta{n}^{2}x\right)}^2-4ta{n}^{2}x}{{\left(1-ta{n}^{2}x\right)}^2}}$

$=\frac{4tanx\times \left(1-ta{n}^{2}x\right)}{1+ta{n}^{4}x-2ta{n}^{2}x-4ta{n}^{2}x}$

$=\frac{4tanx\left(1-ta{n}^{2}x\right)}{1-6ta{n}^{2}x+ta{n}^{4}x}$

= R.H.S.

 

Q24. cos 4x = 1 – 8sin²x cos²x

A.24. L.H.S. = cos 4x.

= cos 2(2x)

= 1 – 2 Sin²(2x) [ cos 2x = 1 – 2 Sin²x]

= 1 – 2 [2 sin xcosx]²[ sin 2x = 2 sin xcos x]

= 1 – 2 [4 sin²xcos²x]

= 1 – 8 sin²xcos²x

= R.H.S.

 

Q25. cos 6x = 32 cos⁶x – 48cos⁴x + 18 cos²x – 1

A.25. L.H.S. = cos 6x

= cos 3(2x)

= 4 cos³2x – 3 cos 2x                 [Q cos 3A = 4 cos³A – 3cos A]

= 4[(2 cos²x – 1)³] – 3[(2 cos²x – 1)]                      [Q cos 2x = 2 cos²x – 1]

= 4[(2 cos²x)³  + 3[(2 cos²x)²(–1) + 3(2 cos²x)(–1)² + (–1)³] – 3(2 cos²x) + 3

{Q (a + b)³= a³ + b³ + 3a²b + 3ab²}

= 4[8 cos⁶x – 12 cos⁴x + 6cos²x – 1] – 6 cos²x + 3.

= 32 cos⁶x – 48 cos⁴x + 24 cos²x – 4 – 6cos²x + 3

= 32 cos⁶x – 48 cos⁴x + 18 cos²x – 1

= R.H.S.

 

Exercise 3.4

Find the principal and general solutions of the following equations:

sin  $\frac{6x}{2}$ sin  $\frac{2x}{2}$ = 0

sin 3x sin x = 0.

sin 3x = 0 or sin x = 0

3x = nπ or x = nπ, n € z,

x =  $\frac{n\pi }{3}$ or x = nπ, n € z,

 

Q6. cos 3x + cos x – cos 2x = 0

A.6. We have,

cos 3x + cosx-cos 2x = 0.

(cos 3x + cosx) cos 2x = 0

Using cos A + cos B = 2 cos $\frac{A+B}{2}$ cos  $\frac{A-B}{2}$

2 cos  $\left(\frac{3x+x}{2}\right)$ cos  $\left(\frac{3x-x}{2}\right)$ - cos 2x = 0.

2 cos  $\frac{4x}{2}$ cos  $\frac{2x}{2}$ - cos 2x = 0

2 cos 2xcosx - cos 2x = 0

cos 2x. (2 cosx - 1) = 0.

cos 2x = 0 or 2 cosx -1 = 0.

2x = (2n + 1)  $\frac{\pi }{2}$ , n∈z or cosx =  $\frac{1}{2}$ = cos  $\frac{\pi }{3}$

x = (2n + 1)  $\frac{\pi }{4}$ , n∈z or x = 2nx±  $\frac{\pi }{3}$ , n∈z.

 

Q7. sin 2x + cos x = 0

A.7. We have,

sin 2x + cosx = 0.

2 sin cosx + cosx = 0(  $\because$ sin 2x = 2 sin xcosx)

cosx (2 sin x + 1) = 0.

cosx = 0     or 2 sinx + 1 = 0.

x = (2n + 1)  $\frac{\pi }{2}$ , n∈z or sin x = $\frac{1}{2}$ = -sin  $\frac{\pi }{6}$ = sin  π + $\frac{\pi }{6}$= sin  $\frac{7\pi }{6}.$

x = (2n + 1)  $\frac{\pi }{2}$ , x∈z or x= nπ + (-1)ⁿ $\frac{7\pi }{6},$ n∈z.

 

Q8. sec²2x = 1– tan 2x

A.8. We have,

sec² 2x = 1 tan 2x

1 + tan² 2x = 1 tan 2x[ sec²x = 1 + tan²x]

tan² 2x + tan 2x = 0.

tan 2x (tan 2x + 1) = 0.

tan 2x = 0         or         tan 2x + 1 = 0.

2x = nπ, x∈z or tan 2x = -1 = -tan $\frac{\pi }{4}$ = tan π- $\frac{\pi }{4}$  = tan  $\frac{3\pi }{4}.$

x=  $\frac{n\pi }{2}$ , n∈z or 2x = nπ + $\frac{3\pi }{4}$ , n∈z.

x =  $\frac{n\pi }{2}+\frac{3\pi }{8},$ n∈z

 

Q9. sin x + sin 3x + sin 5x = 0

A.9. We have,

sinx + sin 3x + sin 5x = 0.

(sinx + sin 5x) + sin 3x = 0.

Using sin A + sin B = 2 sin  $\frac{A+B}{2}$ cos  $\frac{A-B}{2}$ .

2 sin  $\left(\frac{x+5x}{2}\right)$ cos  $\left(\frac{x-5x}{2}\right)$ + sin 3x = 0.

2 sin  $\frac{6x}{2}$ cos $\frac{-4x}{2}$  + sin 3x = 0.

2 sin 3xcos (-2x) + sin 3x = 0.

sin 3x [2 cos 2x + 1] = 0[  $\because$ cos (-x) = cosx].

sin 3x = 0 or 2 cos 2x + 1 = 0.

3x = nπ, n∈z. or cos 2x = $\frac{-1}{2}$ = -cos  $\frac{\pi }{3}$ = cos  π - $\frac{\pi }{3}$= cos  $\frac{2\pi }{3}$

x=  $\frac{n\pi }{3}$ , n∈z or 2x = 2nπ± $\frac{2\pi }{3}$ .

x = nπ± $\frac{\pi }{3}$ , n∈z.

 

Miscellaneous Exercise

Q1.  $2cos\frac{\pi }{13}cos\frac{9\pi }{13}+cos\frac{3\pi }{13}+cos\frac{5\pi }{13}=0$

A.1. L.H.S. = 2 cos $\frac{\pi }{13}$ cos  $\frac{9\pi }{13}$ + cos  $\frac{3\pi }{13}$ + cos  $\frac{5\pi }{13}$ =∂ .

= 2 cos  $\frac{\pi }{13}$ cos  $\frac{9\pi }{13}$ + 2 cos  $\begin{array}{l}\left(\frac{3\pi }{13}+\frac{5\pi }{13}\right)\\ \bar{2}\end{array}$ cos  $\frac{\left(\frac{3\pi }{13}-\frac{5\pi }{13}\right)}{2}$

$\left[\because cosA+cosB=2cos\frac{A+B}{2}cos\frac{A-B}{2}\right]$

= 2 cos  $\frac{\pi }{13}$ cos  $\frac{9\pi }{13}$ + 2. cos  $\left(\frac{8\pi /13}{2}\right)$ cos  $\left(\frac{-2\pi /13}{2}\right)$

= 2 cos  $\frac{\pi }{13}$ cos  $\frac{9\pi }{13}$ + 2 cos  $\frac{4\pi }{13}$ cos  $\frac{\pi }{13}$ [  $\because$ cos (x) = cosx].

= 2 cos  $\frac{\pi }{13}$  $\left[cos\frac{9\pi }{13}+cos\frac{4\pi }{13}\right].$

= 2 cos  $\frac{\pi }{13}\left[2\cdot cos\left(\frac{\frac{9\pi }{13}+\frac{4\pi }{13}}{2}\right)cos\left(\frac{\frac{9\pi }{13}-\frac{4\pi }{13}}{2}\right)\right]$

= 2 cos  $\frac{\pi }{13}$  $\left[2·cos\left(\frac{13\pi /13}{2}\right)cos\left(\frac{5\pi /13}{2}\right)\right]$

= 2 cos  $\frac{\pi }{3}$ × 2 ×cos $\frac{\pi }{2}$ × cos $\frac{5\pi }{26}$ .

= 2 cos  $\frac{\pi }{2}$ 2× 0×cos  $\frac{5\pi }{26}$

= 0

= R.H.S.

 

Q2. (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0

A.2. L.H.S = (sin 3x + sin x) + sin x + (cos 3x - cosx) cosx.

Using

Sin A + sin B = 2 sin  $\frac{A+B}{2}$ cos  $\frac{A-B}{2}$

cos A - cos B = -2 sin $\frac{A+B}{2}$ sin  $\frac{A-B}{2}$ .

L.H.S. =  $\left(2sin\frac{3x+x}{2}cos\frac{3x-x}{2}\right)$ sin x +  $\left(-2sin\frac{3x+x}{2}sin\frac{3x-x}{2}\right)$ cosx

= 2 sin  $\frac{4x}{2}$ cos  $\frac{2x}{2}$ sin x -2 sin  $\frac{4x}{2}$ sin  $\frac{2x}{2}$ cosx.

= 2 sin 2xcosx sin x -2 sin 2x sin xcosx

= 0 = R.H.S.

 

Q3. (cos x + cos y)² + (sin x – sin y)= 4 cos² $\frac{x+y}{2}$

A.3. L.H.S. = (cos x + cos y)² + (sin x- sin y)²

Using,

cos A + cos B = 2 cos  $\frac{A+B}{2}$ cos $\frac{A-B}{2}$

sin A - sin B = 2 cos $\frac{A+B}{2}$ sin  $\frac{A-B}{2.}$

L.H.S. =  ${\left[2\cdot cos\frac{x+y}{2}cos\frac{x-y}{2}\right]}^2+{\left[2cos\frac{x+y}{2}sin\frac{x-y}{2}\right]}^2$ .

= 4. cos² $\left(\frac{x+y}{2}\right)$ cos² $\left(\frac{x-y}{2}\right)$ .. + 4 cos² $\left(\frac{x+y}{2}\right)$ sin² $\left(\frac{x-y}{2}\right)$ .

= 4 cos² $\left(\frac{x+y}{2}\right)$  $\left[co{s}^2\left(\frac{x-y}{2}\right)+si{n}^2\left(\frac{x-y}{2}\right)\right]$

= 4 cos² $\left(\frac{x+y}{2}\right)$ [  $\because$ cos²∅+ sin²q∅  = 1].

= R.H.S.

L.H.S =

 

Q4. (cos x – cos y)²+ (sin x – sin y)² = 4 sin² $\frac{x-y}{2}$

A.4. L.H.S = (cos x-cos y)² + (sin x- sin y)²

=  ${\left[-2sin\frac{x+y}{2}sin\frac{x-y}{2}\right]}^2+{\left[2cos\frac{x+y}{2}sin\frac{x-y}{2}\right]}^2$

= 4 sin² $\left(\frac{x+y}{2}\right)$ sin² $\left(\frac{x-y}{2}\right)$ + 4 cos² $\left(\frac{x+y}{2}\right)$ sin² $\left(\frac{x-y}{2}\right)$

= 4 sin² $\left(\frac{x-y}{2}\right)$  $\left[si{n}^2\left(\frac{x+y}{2}\right)+co{s}^2\left(\frac{x+y}{2}\right)\right]$

= 4  $si{n}^2\left(\frac{x-y}{2}\right)$ ..[  $\because$ sin²∅ + cos²∅= 1]

= R.H.S.

 

Q5. sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x

A.5. L.H.S = sin x + sin 3x + sin 5x + sin 7x.

= (sin x + sin 7x) + (sin 3x + sin 5x)

Using,

sin A + sin B = 2 sin  $\frac{A+B}{2}$ cos  $\frac{A-B}{2}.$

L.H.S. = 2. Sin  $\frac{x+7x}{2}$ cos  $\frac{x-7x}{2}$ + 2 sin $\frac{3x+5x}{2}$ cos  $\frac{3x-5x}{2}$

= 2 sin  $\frac{8x}{2}$ cos  $\left(-\frac{6x}{2}\right)$ + 2 sin  $\frac{8x}{2}$ cos  $\left(-\frac{2x}{2}\right)$

= 2 sin 4x cos 3x + 2 sin 4x cosx.[  $\because$ cos (-x) = cosx]

= 2 sin 4x[cos 3x + cosx]

Using cos A + cos B = 2 cos  $\frac{\mathrm{A\; +}B}{2}$ cos  $\frac{A-B}{2}.$

So, L.H.S. = 2 sin 4x  $\left[2·cos\frac{3x+x}{2}cos\frac{3x-x}{2}\right].$

= 2 sin 4x  $\left[2·cos\frac{4x}{2}·cos\frac{2x}{2}\right]$

= 4 sin 4x. cos 2x cosx = R.H.S.

 

Q6.  $\frac{\left(sin7x+sin5x\right)+\left(sin9x+sin3x\right)}{\left(cos7x+cos5x\right)+\left(cos9x+cos3x\right)}=tan6x$

A.6. L.H.S. = $\frac{(sin7x+sin5x)+(sin9x+sin3x)}{(cos7x+cos5x)+(cos9x+cos3x)}.$

Using sin A + sin B = 2 sin  $\frac{A+B}{2}$ cos  $\frac{A-B}{2}$

cos A + cos B = 2 cos  $\frac{A+B}{2}$ cos  $\frac{A-B}{2}.$

 

Q7. sin 3x + sin 2x – sin x = 4sin x $cos\frac{x}{2}cos\frac{3x}{2}$

A.7. L.H.S = sin 3x + sin 2x - sin x

= sin 3x - sin x + sin 2x.

= 2 cos  $\frac{3x+x}{2}$ .. sin  $\frac{3x-x}{2}$ + sin 2x  $\left[\because sinA-sinB=2cos\frac{A+B}{2}sin\frac{A-B}{2}\right]$

= 2 cos  $\frac{4x}{2}$ sin  $\frac{2x}{2}$ + sin 2x.

= 2 cos 2x sin x + 2 sin xcosx        [ $\because$ sin 2x = 2sin xcosx]

= 2 sin x [cos 2x + cosx]

= 2 sin x  $\left[2cos\frac{2x+x}{2}cos\frac{2x-x}{2}\right]$  $\left[\because cosA+cosB=2cos\frac{A+B}{2}cos\frac{A-B}{2}\right]$

= 2 sin x  $\left[2.cos\frac{3x}{2}cos\frac{x}{2}\right]$

= 4 sin xcos  $\frac{x}{2}$ . cos  $\frac{3x}{2}$ = R.H.S.

Find sin  $\frac{x}{2}$ , cos  $\frac{x}{2}$ and tan  $\frac{x}{2}$ in each of the following :

 

Q8. tan x = − $\frac{4}{3}$ , x in quadrant II

A.8. We have, tan x= $\frac{-4}{3}$ , x in IInd quadrant.

Since,  $\frac{\pi }{2}<x<\pi$

$\frac{\pi }{4}<\frac{x}{2}<\frac{\pi }{2}$

sin  $\frac{x}{2}$ , cos  $\frac{x}{2}$ , tan  $\frac{x}{2}$ are all positive.

Now, sec²x = 1 + tan²x = 1 + ${\left(\frac{-4}{3}\right)}^2$ = 1 +  $\frac{16}{9}$ =  $\frac{9+16}{9}$ =  $\frac{25}{9}$

secx = ± $\frac{5}{3}$

cosx = ± $\frac{3}{5}$ .

cosx =  $\frac{-3}{5}$ as x is in IInd quadrant.

Now, 2 sin².. = 1 cosx.    [cos 2x = 1 2 sin²x.]

2 sin² $\frac{x}{2}$ = 1  $\left(\frac{-3}{5}\right)$

2 sin² $\frac{x}{2}$ =  1 + $\frac{3}{5}$=  $\frac{5+3}{5}$ =  $\frac{8}{5}$ .

sin² $\frac{x}{2}$ =  $\frac{8}{2\times 5}$ =  $\frac{4}{5.}$