Rachit Kumar SaxenaManager-Editorial
What is Linear Function?
When a function’s variables do not have an exponent, then it is said to be a linear function. There are either one or two variables in a linear function, but if there are more variables, they are either known variables or constant.
Define Linear Function
The graph of a linear function can be represented as a straight line. It is a polynomial function that has a degree of 0 or 1. The below-mentioned formula can give its expression:
y = f(x) = px + q
Here, y is the dependent variable, whereas x is the independent variable, and p is the term that remains constant.
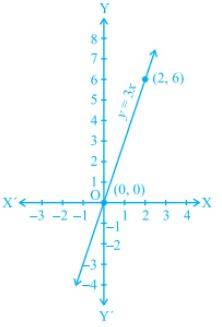
Graph of a Linear Function
Follow these to draw a graph of a linear function:
Find 2 points that satisfy the linear function’s equation y = px + q and mark these points in an XY-plane.
Now, just join those points with a line.
Check the below image for a better understanding.
Slope of a Linear Function
If a linear function has variables x and y, the change of the value of y as x changes remain the same. The rate at which y changes concerning x is called the slope of a linear function.
For example, check the below table to examine the change in y with respect to x
| x |
y |
|---|---|
| 0 |
4 |
| 1 |
5 |
| 2 |
6 |
By examining this table, you can see that the rate of change is 4. This can be represented by a linear function y = x + 4, and 4 will be its slope.
Weightage of Linear Functions in Class X and XI
How to draw a graph using the linear function and related concepts is taught in Class X, and it carries a weightage of 5 marks in the exam.
Class XI comprises more difficult problems related to linear functions, and this topic carries a weightage of up to 4 marks in the exam.
Illustrative Examples of Linear Functions
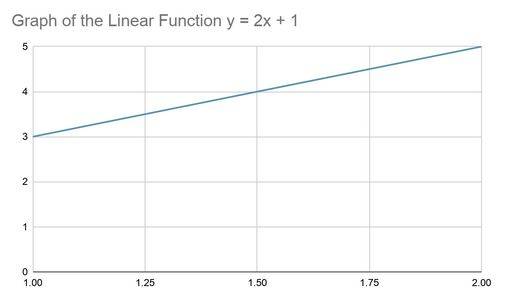
1.Find the graph of linear function y = 2x + 1
Solution.
For x = 1, y = 2 x 1 + 1 = 3
For x = 2, y = 2 x 2 + 1 = 5
2. Ajay makes Rs. 500 for every watch he sells. It has a fixed cost of Rs. 400 and its variable cost is Rs. 50. How much profit will he make by selling 25 watches?
Solution.
R(x) = 500x
C(x) = 400 + 50x
Therefore, P(x) = 500x - (400 + 50x) = 450x - 400
When x = 25, the profit he will make is = 11250 - 400 = 10850.
3. A company makes a product at a fixed cost of Rs. 500 and the variable cost of Rs. 100. Calculate the total cost after manufacturing varying units.
Solution.
Let x = manufactured units and A = total cost.
Therefore, A = Fixed Cost + Variable Cost = 500 + 100x
Suppose that the company manufactures 5 and 10 units respectively. The below table shows the total cost for each manufacturing batch or output.
| Output |
Total Cost = 500 + 100x |
| 5 |
A = 500 + 100(5) = 1000 |
| 10 |
A = 500 + 100(10) = 1500 |
Therefore, the company spends Rs. 1000 and Rs. 1500 after manufacturing 5 and 10 units, respectively.
FAQs on Linear Function
Q: Who is the founder of linear equations?
Q: Define Nonlinear Function and give some examples.
Q: Who can make use of linear functions?
Q: What is the difference between exponential and linear functions?
Q: Is logarithmic functions linear?
News & Updates
Relations and Functions Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test