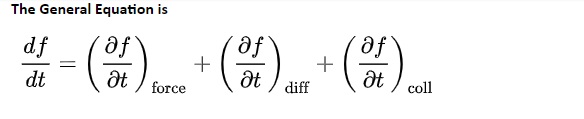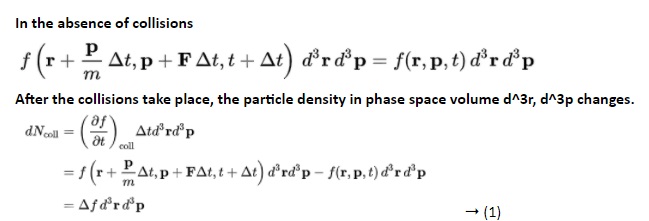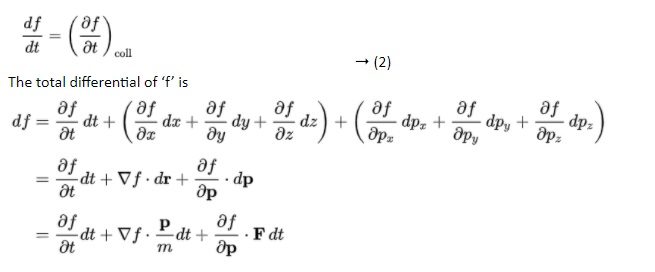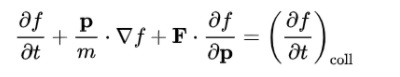Introduction
If we take a hot, dense gas, the large numbers of atoms collide with each other, leading to the excitation to the various energy levels. After some time scales, molecules exhibit radiative de-excitation. At constant temperature and pressure, equilibrium built between the collisional excitations and radiative deexcitations.
- The equilibrium leads to the distribution of atoms between the energy levels. At higher temperatures, the large number of atoms occupy at high energy levels.
- Thus the Boltzmann equation shows the distribution of atoms among different energy levels as a function of energy and temperature.
Boltzmann Equation
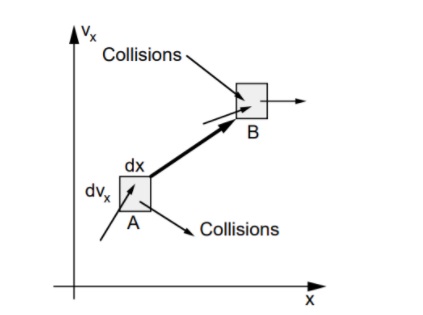
The Boltzmann equation helps us to define the properties of dilute gases. It analyses the elementary collision processes between a pair of molecules. In general, the Boltzmann equation is expressed as a kinetic equation that describes the change of macroscopic quantity in a thermodynamic system, such as energy, charge or particle number.
Distribution Functions
- A plasma is an ensemble of particles electrons ‘e,’ ions ‘i’ and neutrals ‘n’ with different positions ‘r’ and velocities ‘v,’ which move under the influence of external forces (electromagnetic fields, gravity) and internal collision processes (ionisation, Coulomb, charge exchange)
- The macroscopic plasma parameters are j - current density, ne - electron density, P - pressure, and Ti - ion temperature.
The Boltzmann Equation for Class 11
In chapter ‘Thermodynamics,’ the Boltzmann equation has less probability than other thermodynamics laws. The Boltzmann equation is an elaborated topic with different applications in physics. The weightage of this topic is below 5 marks.
FAQs on Boltzmann Equation
Q: What are the applications of the Boltzmann equation?
Q: What is the Maxwell-Boltzmann distribution?
Q: What is the Collisionless Boltzmann Equation?
Q: What is the convective derivative?
Q: What is the Boltzmann Planck equation?
Q: What are the macroscopic variables?
News & Updates
Thermodynamics Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test