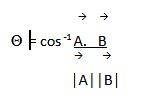Angle between Two Vectors: Overview, Questions, Preparation

A quantity that has magnitude, as well as direction, is called a vector. However, scalar quantities have a magnitude and no direction. A vector can be represented in two forms, i.e., in two dimensions and three dimensions.

How to find an angle between two vectors?

To find the angle between two vectors, one needs to follow the below steps:

Step 1 – Estimate the dot product of the given vectors with the use of the following formula:

→ →

A. B   = A_xB_x + A_yB_y + A_zB_z

Step 2 – Calculate the magnitude of both the numbers separately. The method to calculate the magnitude is squaring all the vectors’ components and adding them together and finding the result’s square roots.

Step 3 – The last step would be substituting the values of the dot product and the magnitude of both the vectors, i.e.

Importance of Angle Between two Vectors

 The Vector Algebra chapter in the NCERT Class XII Maths includes some key topics such as:

• Vectors and scalars (direction and magnitude of a vector)
• Direction cosines and ratios of a vector
• The position vector of a point dividing a line segment in a given ratio
• Properties and application of scalar product of vectors (dot), vector product of vectors (cross), and scalar triple product of vectors

The angle between the two vectors is an essential topic in class XII. The chapter Vectors carries 12 marks in Final Examination. Students may expect around 2-4 marks questions from this topic. 

Some of the examples of angle between two vectors are as below:

1. Calculate the angle between two vectors 3i + 4j and 2i – j + k

Solution.

→                         →

a = 3i + 4j – k and b = 2i – j + k

The dot product is defined as:

→  →

a .  b = (3i + 4j – k).(2i – j + k)

= (3)(2) + (4)(-1) + (-1)(1)

=6-4-1

=1

          →   →

Thus,  a .   b = 1

The magnitude of vectors is given as below:

   →

  │a│= √(32 + 42 + (-1)2) = √26 =   5.09

   →

  │b│= √(22 + (-1)2 + 12) = √6 =     2.45

 The angle between the two vectors is as follows:

             →   →

 = cos^-1 A.   B 

           →    →

          │A││B│

=cos^-1 1 /(5.09)(2.45)

= cos^-1 1/12.47

 = cos^-1 (0.0802)

 = 85.39°

2. Compute the angle between two vectors 5i - j + k and i + j - k

Solution.

→                       →

a = 5i - j + k and b = i + j - k

 The dot product is defined as:

→    →

  a .   b = (5i - j + k)(i + j - k)

= (5)(1) + (-1)(1) + (1)(-1)

=5-1-1

=3

         →  →

Thus, a . b    = 1

The magnitude of vectors is given as below:

    →

  │a│= √(52 + (-1)2 + 12) = √27 =   5.19

   →

 │b│= √(12 + 12 + (-1)2) = √3 =     1.73

 The angle between the two vectors is as follows:

              →   →

 =   cos^-1A.  B

             →       →          

             │A││B│

 = cos^-1 3 /(5.19)(1.73)

  = cos^-1 3 / 8.97

 = cos^-1 (0.334)

 = 70.48°

Q: What are the different types of vectors?

Q: Which are the major topics covered in Class XII Maths Chapter 10 in the NCERT syllabus?

Q: What is the difference between vector and scalar?

Q: What will the students learn from the 10th Chapter of Class XII of NCERT syllabus?

Q: What is equality of vectors?