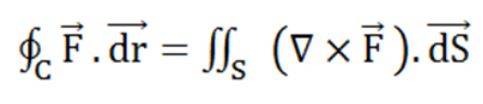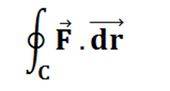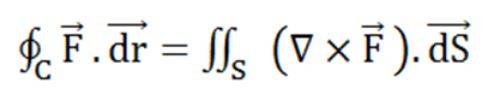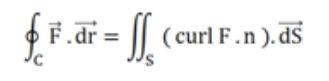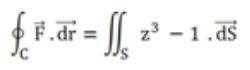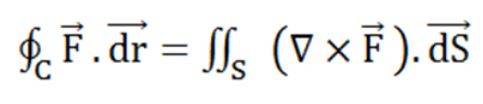Stokes Theorem: Overview, Questions, Preparation

This chapter has multiple topics listed below:

Vector Algebra Stokes Theorem Angle between Two Vectors Dot Product Parallelepiped Unit Vector Vector Space Vector Addition Parallelogram Law Magnitude of a Vector Scalar Triple Product Types of Vectors Vector Calculus Vector Product Components of a Vector

Rachit Kumar SaxenaManager-Editorial

Updated on Jun 29, 2021 09:22 IST

Table of Contents

What is Stokes Theorem?
Weightage of Stoke’s theorem
Illustrative Examples on Stokes Theorem
FAQs on Stoke's Theorem

What is Stokes Theorem?

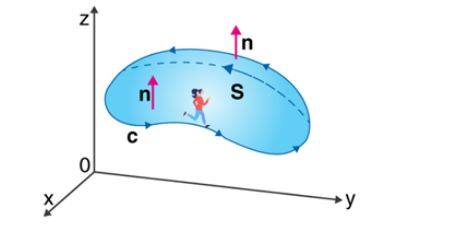
Stoke's Theorem is an important theorem that shows the relationship between a line and a surface integral of vector fields. It mainly states that the surface integral of a function's curl over a surface bounded by a closed surface is always equal to the line integral of the particular vector function around that surface.

Formula:

The formula for Stoke's Theorem is:

Here,
C indicates a closed curve.
S indicates any surface surrounded by C.
F is a vector field whose components have constant derivatives in R3's open region containing S.

Weightage of Stoke’s theorem

Stoke's theorem is an essential topic of chapter Vector Algebra. Chapter Vector Algebra if present in class XII. Vector Algebra is a necessary topic as per the class XII examinations and the other competitive exams. The chapter's weightage in class XII examinations ranges from 7 to 10 marks. And 3 to 5 questions having moderate to difficulty level are always asked in class XII exams.

The importance of the topic stoke's theorem is majorly present in higher studies and other competitive exams. Stoke's theorem mainly uses applications of vectors and calculus. In the chapter of Vector Algebra, other topics are also present, such as:

Various kinds of Vectors
Addition of similar or different Vectors
Multiplication of a Scalar and Vector
Product of two same or different vectors

Illustrative Examples on Stokes Theorem

1. Compute

where F = y i + xz³ j - zy³ k. And C is the circle oriented in an anti-clockwise manner and is present in the plane z = -3, x²+y² ≤ 4.

Solution.

We know the formula for stoke's theorem is

where n is the normal vector,

The value for curl(F)* n = [d(xz3)/dx - d(y)/dy] = z3 -1,
z = -3 (given), therefore z3 -1 = -27 - 1 = -28
Now,

2. Prove that the line integral ∮C yz.dx + xz.dy + xy.dz is 0 along the closed surface C.
Solution.

For a closed surface C let S be its bounded surface.

As per the Stoke's formula, we can see that P = yz, Q = xz, R = xy.

Therefore,

∇×F = (dR/dy - dQ/dz) i + (dP/dz - dR/dz) j + (dQ/dz - dP/dy) k,

After solving this we will get 0 i + 0 j + 0 k = 0.

Hence putting the value of ∇×F into the Stoke's formula,

we will get zero.
Hence by this, it is proved that the line integral for the statement is zero.

3.What will happen if a Sphere has no boundary?
Solution.

If a sphere does not have any boundary present, then the line integral across the object's boundary will be zero.

FAQs on Stoke's Theorem

Q: Write the Stoke's Theorem in the coordinate form.

Q: Which operation is used in Stoke's Theorem?

A: Curl Operation is used in the respective theorem.

Q: Mention the primary difference between Stoke's Theorem and Green's Theorem.

A; Stoke's theorem shows the Surface Integral relationship across a surface and the line integral over the plane boundary curve.
Green Theorem explains the relationship between the double integral across the surface and line integral over the curved surface's boundary.

Q: When was Stoke's theorem invented?

A: 1850

Q: How can we use Stoke's theorem?

A: We can use the theorem in converting the Surface integrals through a vector field into line integrals.