Vector Addition: Overview, Questions, Preparation

This chapter has multiple topics listed below:

Vector Algebra Stokes Theorem Angle between Two Vectors Dot Product Parallelepiped Unit Vector Vector Space Vector Addition Parallelogram Law Magnitude of a Vector Scalar Triple Product Types of Vectors Vector Calculus Vector Product Components of a Vector

Rachit Kumar SaxenaManager-Editorial

Updated on Jun 30, 2021 02:13 IST

Table of Contents

What is a Vector Addition?
Weightage of Vector Addition
Illustrative Example of Vector Addition
FAQs on Vector Addition

What is a Vector Addition?

Any entity that has magnitude and position is a vector. Examples of vector quantities are displacement, velocity, acceleration, force, strain, etc. Mathematical operations can be done between two or more vectors.

Vector Addition

The method of adding two or more vectors is called vector addition. Depending on the position of the vector, the addition of the vector is divided into two groups.
They're –

Law of the parallelogram of vector addition

Triangular law of addition of vector

Consider vector A and vector B

The form of vector inclusion is selected based on the configuration of the vector head and tail.

If two vectors are arranged head to tail, the triangular rule of vector addition shall be followed.

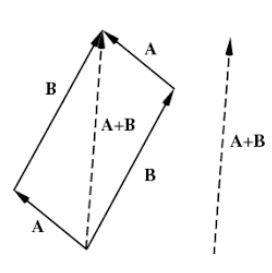
Law of the Parallelogram of Vector Addition

If two vectors are arranged head to head or tail to tail so parallelogram rule of vector addition shall be applied.

Statement: If we consider two vectors as the adjacent sides of a parallelogram, the result is a diagonal vector cutting through two vectors' contact point.

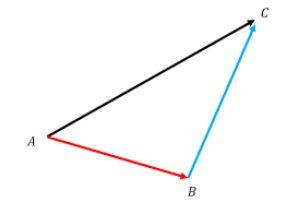
Triangular Law of Addition of Vectors

If two vectors are arranged head to tail, the triangular rule of vector addition shall be applied.

Statement: When two sides of a triangle represent two vectors in direction and magnitude in the same order, then the third side of that triangle represents the resultant vector in direction and magnitude.

Why is Vector Addition Important?

In mathematics, the quantity of vectors like force combines and creates an effect on which they are applied. As the effect of all these forces is taken into account when deciding the purpose of the mechanism's motion, certain processes, such as addition, subtraction, and multiplication, are essential to determine the outcome of these forces.

Weightage of Vector Addition

This concept is taught in chapter Vector Algebra. You will learn about the basics of vectors, their addition, and subtraction. The weightage of this chapter is 14 marks.

Illustrative Example of Vector Addition

1. Two forces of 3 N and 4 N operate when the angle between them is 60 degrees. Find the resultant force that arises from this.

Solution.

Resultant force, R = √(42 + 32 + 2 x 3 x 4 Cos 60°)

= √(9 + 16 + 12)

= √(37 = 6.08 N

The direction of R =

tan q = (3 Sin 60°)/(4 + 3 Cos 60°) = 0.472

q = tan^-1 0.472

= 25.3°

2. Find the x and y components with a displacement of 25 m at an angle of 210 deg.

The horizontal axis angle is 210 deg-180 deg = 30 deg.

Component x = OB =-25 Cos 30°= -21.7

Component Y = AB =-25 Sin 30° = -12.5 m

Remember that each component points along the negative coordinate path, so we have to take it as negative.

FAQs on Vector Addition

Q: When are we going to use the parallelogram rule of vector addition?

A: We use the parallelogram rule of vector addition when the tail of the two vectors join at a common point or their heads join at a common point.

Q: State parallelogram law of addition of vectors.

A: If two vectors are assumed to be the opposite sides of a parallelogram, the resultant of two vectors is a diagonal vector going across two vectors' contact point.

Q: State triangular law of the addition of vectors.

A: Suppose two sides of the triangle define two vectors in direction and magnitude in the same order. In that case, the third side of the triangle represents the resultant vector in direction and magnitude.

Q: What is the resulting vector in the parallelogram law of vector addition?

A: In the parallelogram rule of vector addition, the diagonal represents the resulting vector.

A: When two vectors are arranged head-to-tail. To calculate the corresponding vector, the triangular law of vector addition is applied.