Components of a Vector: Overview, Questions, Preparation

The physical quantities by which both magnitude and direction are clearly specified are known as vector quantities. Vectors are denoted by placing an arrow over the denotations describing them. For example, to describe a vehicle's acceleration, its direction must also be defined along with its magnitude. It can be expressed as a-m/s2 in vector form. Vectors can be conveniently described in three dimensions using the coordinate scheme. 

The elements of a vector are commonly called x-component and y-component in the two-dimensional coordinate scheme. It can be shown as V = (vx, vy), where the vector is V. These are the vector components produced along the axes. Using the formula for both two-dimensional and three-dimensional coordinate structures, we can find the components of any given vector. 

Source: NCERT

Components of a Vector 

Suppose the vector V in a two-dimensional plane is described. Vector V is divided into two sections, such as vx and vy. 
An angle is now created between the vector V and the vector x-component. When we draw a line parallel to the y-component, the vector V and its x-component (vx) form a right-angled triangle (vy). 

By trigonometric ratios, 
cos θ = Adjacent Side/Hypotenuse = vx/V
sin θ = Opposite Side/Hypotenuse = vy/V

Where V is the vector's magnitude V. 

Vector Formula Components 
As we have obtained the expression in the previous section: 
vx/V = cos θ   
vy/V = sin θ

The method for finding the components of any given vector therefore becomes: 
Vx=V cos θ
Vy=V sin θ

Where V is the variable V magnitude, which can be found using the Pythagoras theorem; 
|V| = (vx^2, vy^2) 

Orthogonal Vectors

Using the Coordinate Scheme in three dimensions, vectors can be conveniently interpreted. Let us understand what orthogonal representation is before getting into the representation of vectors. 

In terms of coordinate geometry, we say parameters are at right angles to each other by orthogonal representation. We have three axes perpendicular to each other in the orthogonal three-dimensional structure, reflecting the axes of x, y, and z. 

We can have three distinct unit vectors in orthonormal or orthogonal structures, with one in each direction.

Vector Component Form 
Any vector p can be represented in terms of its unit vectors in the Cartesian Coordinate Scheme. The unit vectors are given by î, ĵ, and k̂, respectively, in the direction of x,y, and z-axes. With respect to the origin of the defined coordination scheme, the location of vector p can be interpreted in space as: 
p = xî + yĵ + zk̂

This topic is taught in the chapter Vector Algebra. You will learn about the form and types of vectors. The weightage of this chapter is 8 marks. 

1. For a force of 20 Newtons, the x-axis angle is 30o. Find all the force elements of x and y. 
Solution.
Fx = F cos 30°
= (20)(cos 30°) 
= (20)(0.5√3) 
= 10√3 Newton 

Fy = F sin 30°
= (20)(sin 30°) 
= (20)(0.5) 
= 10 Newton 

2. Consider the vector from the origin to (3, 5). What will be the reflection of a variable that had a magnitude of -2 times that? 
Solution.
Here, the target section v from (0, 0) to (3, 5) is k=-2. 

Kv=(−2(3),−2(5))=(−6,−10) 

Since k

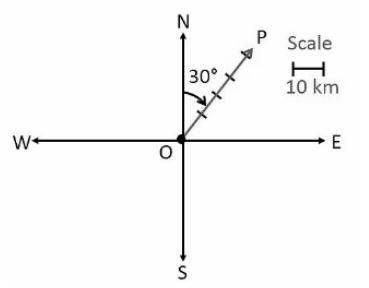
3. Represent graphical displacement of 40 km, 30° east of north.
Solution:

 
OP→  represents the displacements of 40 km, 30° east of north.

Q: Define polar vector. 

Q: What is a unit vector's magnitude? 

Q: What is a zero vector magnitude? 

Q: When will the two vectors be assumed to be equal? 

Q: When a vector is multiplied by a positive number, what happens to the direction?