Dot Product: Overview, Questions, Preparation

A vector is defined as a quantity that has magnitude as well as direction. The length connecting the beginning and final points of a vector is known as the magnitude of the vector. The types of vectors are zero vector, unit vector, coinitial vector, collinear vector, and equal vector.

Product of Vectors:

Multiplication of two vectors is defined in the following ways:

Scalar product (or dot product) where the result is a scalar.

Vector product (or cross product) where the result is a vector.

Dot Product of Two Vectors:

The dot product of two vectors signifies their orientation with respect to each other. It represents the intensity of vectors in a numeric form. The dot vector also shows the amount of effect one vector has on the other, be it negative, positive, or zero.

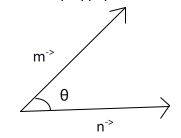
The scalar product of two non-zero vectors, denoted by
m.n = |m||n|cos θ

where θ is the angle between m and n. 

Properties

1. The dot product follows commutative property. It means that the order of their product does not affect the result of the multiplication. m.n = n.m = mn cos θ= nm cos θ
2. The zero property indicates that if m.n is zero, then either m or n is zero. Or, cos θ  must be zero. If cos is zero, then = /2 which indicates perpendicularity.
3. The scalar property shows that. (mp).(nq) = (mq).(np) = mn p.q
4. A vector’s dot product with itself is merely the square of its magnitude. m.m= m.m cos θ = m²
5. The distributive property of dot product is- m.(n + p) = m.n + m.p 

The topic- Dot product is a part of the chapter- vector algebra. This chapter holds a weightage of 6-8 marks in class 12 examinations.

1.Given, two vectors [5,3,-2] and [6,-4,3]. Find their dot product.

Solution.
The given vectors are [5,3,-2] and [6,-4,3].
So, dot product= P= (a1.a2) + (b1.b2) + (c1.c2)
P= (5 x 6) + (3x (-4)) + ((-2)x 3)= 30- 12- 6= 30- 18= 12.

2.Two vectors m and n form an angle of 60 degrees. Their magnitude is 3 and 4, respectively. Calculate the dot product of these two vectors.

Solution.
Given, |m|= 3 and |n|= 4.
Also, angle= =60
The formula to calculate the dot product is-
m.n = |m||n| cos
m.n = 3 x 4 x ½ = 6

3. Calculate the dot product of two vectors m and n, if m= (-3i,-8j) and n= (-2i,3j). Also, find the type of angle made by these two vectors.
Solution.

The given vectors are m= (-3i,-8j) and n= (-2i,3j).

We know that, the dot product of two vectors is given by-

m.n= (m₁,n₁ + m₂n₂)= [(-3i.-2i)+(-8j.3j)]= [(6 i²)+(-24 j²)].

Since i² and j² are unit vectors, their magnitude is one.

So,m.n = (6)+(-24)= -18.

Q: What is the difference between the dot product and cross product?

Q: What is the property of the dot product?

Q: What are the initial point and terminal point of a vector?

Q: What is the orthogonal property?

Q: What are the applications of the dot product?