Collinear Points: Overview, Questions, Preparation

In Euclidean Geometry, three or more points are collinear if they lie on the same line. The word “Collinear” is derived from the Latin words “Col,” meaning together, and “linear,” meaning line. Definition: Collinear points are the points that lie on the same line, whether they are close together, far apart, or form a ray, line segment, or line. 

Example: Students standing in a line for their morning assembly. 

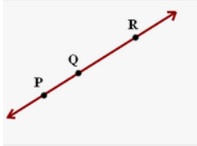
Here, P, Q, and R are collinear points as they lie on the same straight line.

Non-Collinear Points

Points that do not lie on the same line, and don’t connect to form a straight line, are called non-collinear points.
Examples: Points on spirals, points on the globe, etc.

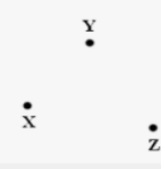
 X, Y, Z does not lie on the same line and are thus non-collinear points.

There are two ways to determine if the points are collinear:

• Slope formula
• Area of triangle

Slope formula

The slope or gradient of a line is a number that describes both the steepness and direction of the line. Three or more points are collinear if the slope of any two pair points is the same. 
For example, for proving that points X, Y and Z are collinear, you first have to prove that X and Y are collinear, and then prove that Y and Z are also collinear. 

The formula is:

m= (y₂-y₁) / (x₂-x₁).

Here, m= slope,

x₁ y₁= coordinates of the first point inline,

x₂ y₂= coordinates of the second point inline.

If the slope of XY= slope of YZ= slope of ZX, then the points X, Y, and Z are collinear. 

Area of triangle

If the area of a triangle formed by three points is zero, then the points are collinear. Non-collinear points can form a triangle, but collinear points cannot.  

For the points A(x₁,y₁) B(x₂,y₂) C(x₃,y₃), the formula used will be:

Area= ½ (x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂) =0

Here, x and y will be coordinates of the points. 

This chapter is taught in Class 10th and carries 6 marks.

1. Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.

Solution. The points are collinear if the sum of any two line segments is equal to the third.

Let A (1, 5), B (2, 3), and C (-2, -11).

AB= √{(2-1)2 + (3-5)2} = √5

BC= √{(-2-2)2 + (-11-3)2}= √212

CA= √{(-2-1)2 + (-11-5)2} = √265

AB + BC ≠ CA.

Hence, the given points are not collinear.

2.Find the coordinates of the point that divides the join of (�V1, 7) and (4, �V3) in the ratio. 

Solution. Let the required point be P (x, y).

Using section formula, 

x= (2*4+3*(-1))/(2+3) = 1,

y= (2*-3+3*7)/(2+3)= 3.

The point is (1,3).

3. Find the ratio in which the line segment joining the points (–3, 10) and (6, –8) is divided by (–1, 6).

Solution.  Let k:1 be the ratio in which the line segment is divided.

Thus, -1= (6k-3)/(k+1),

-k-1=6k-3,

k=2/7.

The required ratio is 2:7.

Q: What are collinear points?

Q: Can two points be collinear?

Q: What is the formula for collinear points?

Q: How to determine collinear points by the slope formula?

Q: What are coplanar points?