Total Probability Theorem: Overview, Questions, Preparation

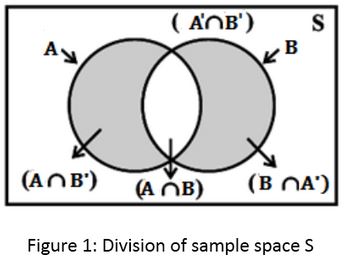
For two occasions A and B related with an example space S, the example space can be separated into a set A ∩ B′, A ∩ B, A′ ∩ B, A′ ∩ B′. This set is supposed to be commonly disjoint or pairwise disjoint because any pair of sets in it is disjoint. Components of this set are also called a parcel of test space.

Statement
Let occasions C1, C2 . . . Cn structure segments of the example space S, where all the occasions have a non-zero likelihood of event. For any occasion, A related with S, as per the all-out likelihood hypothesis, 

P(A) = ∑k=0nP(Ck)P(A|Ck)

Theorem Proof:

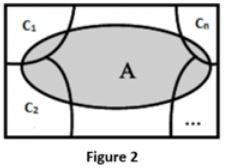
From figure 2, {C1, C2, . . . . , Cn} is the segments of the example space S with the end goal that, Ci ∩ Ck = φ, where I ≠ k and I, k = 1, 2,…,n additionally all the occasions C1, C2 . . . . Cn have non zero likelihood. Test space S can be given as, 

S = C1 ∪ C2 ∪ . . . . . ∪ Cn 

For any occasion A, 

A = A ∩ S 

= A ∩ (C1 ∪ C2∪ . . . . ∪ Cn) 

= (A ∩ C1) ∪ (A ∩ C2) ∪ … ∪ (A ∩ Cn) . . . . . (1) 

We realize that A ∩ Ci and A ∩ Ck are the subsets of Ci and Ck. Here, Ci and Ck are disjoint for I ≠ k. since they are commonly autonomous occasions, which suggests that A ∩ Ci and A ∩ Ck are additionally disjoint for all I ≠ k. Hence, 

P(A) = P [(A ∩ C1) ∪ (A ∩ C2) ∪ … .. ∪ (A ∩ Cn)] 

= P (A ∩ C1) + P (A ∩ C2) + … + P (A ∩ Cn) . . . . . . . (2) 

We realize that, 

P(A ∩ Ci) = P(Ci) P(A|Ci)(By duplication rule of likelihood) . . . . (3) 

Utilizing (2) and (3), (1) can be changed as, 

P(A) = P(C1)P(A| C1) + P(C2)P(A|C2) + P(C3)P(A| C3) + . . . . . + P(Cn)P(A| Cn) 

Subsequently, the hypothesis can be expressed in the type of condition as, 

P(A)=∑k=0nP(Ck)P(A|Ck)

The chapter Probability has explained in-depth all the possible outcomes in sets and unions and the theorem, which helps in dealing with the questions.
The chapter has a weightage of 8 Marks.

1.Theorem of all out likelihood is given by P(A) = P(E1) P(A|E1) + P(E2) P(A|E2) +… ..(n terms).
Solution. True

2. The likelihood that individual A finishes all the undertakings allowed is half, and that of individual B is 20%. Discover the likelihood that all the assignments are finished.
Solution. 0.35

3.The formula for total probability is?
Solution. The likelihood for a can be composed as amounts of occasion B. The all-out likelihood rule is: P(A) = P(A∩B) + P(A∩Bc)

Q: What can be the total probability of an event?

Q: Explain the fundamental laws of probability.

Q: What is a partition theorem?

Q: What is meant by P (A U B)?

Q: In Baye's theorem, is the total probability theorem used?