Probability Density Function: Overview, Questions, Preparation

The Probability Density Function (PDF) is used to describe the potential of a random variable to take on some value within a separate set of values. The article explains the function of a normal distribution, probability density, and how the mean and variance exist.

The Probability Density Function (PDF) is the probability function that is seen between a certain set of values for the density of a continuous random variable. It's sometimes called a function of a probability distribution or simply a function of probability. This function is, however, stated in many other references as the function over a general set of values or often referred to as the cumulative distribution function or sometimes as the probability mass function (PMF). But for continuous random variables, PDF is defined as the reality, while PMF is defined for discrete random variables.

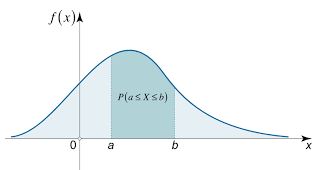
In the case of a continuous random variable, X's probability for a given value of x is always 0. In this case, it does not work if we find P(X = x). Instead, we need to measure the likelihood of X lying within an interval (a, b). Now, for P(a

  P(a _a∫ ^b f(x)

Probability Density Function Applications

Applications of the probability density function include the following:

In modelling, the annual details of atmospheric NOx temporal concentration, the probability density function is used.
It is used to model the combustion of diesel engines.
It is used to measure the odds associated with random variables in statistics.

In the Probability chapter, you will learn about probability density and its properties and application. The weightage of Probability is 5-6 marks in the exam.

1. X is a random variable, and its PDF is given  by 

f(x) = {x²+1; 0; x≥0x

Find P(1 Solution. 
Given,
f(x) = {x²+1; 0; x≥0x1∫³(x2+1)dx

= [x³/ 3+x]³₁ = [(273+3) − (13+1)]

= [(9+3) − 43]

= 36 − 43 = 323

2. Let X be a random variable with PDF given by
           fX(x)={cx2    if |x|≤1  0       otherwise.
Find the constant c.
Solution: 
For finding -_∞∫^∞cx2 dx = 1
Integrating we get,        
2/3c in LHS
So c = 3/2

3.Let X be a continuous random variable with PDF fX(x) = {4x300
Find P(X ≤ 23|X > 13).
Solution:

P(X ≤ 23|X > 13) = P(13 13)

=∫23134x3dx ∫1134x3dx

=316

Q: What does probability density mean?

Q: How can you find the density of probability?