Rachit Kumar SaxenaManager-Editorial
What is Probability Distribution?
Probability is the measure of the chance of occurrence of any event. A list of all the possible outcomes is known as the sample space. If an event E occurs, its probability is denoted by P(E).
The conditional probability of an event occurring concerning the occurrence of another event is given as-
P(M|N)= (Number of events favourable to M N) / (Number of events favourable to N)
= n (M N) / n(N).
Random Variable:
A random variable is a real numbered entity. The domain of a random variable is the sample space of a random experiment.
A descriptive depiction of the values of the random variable along with their associated probabilities is known as the probability distribution of that random variable.
Probability Distribution:
The probability of a random variable V is given as -
V : v1, v2, v3, ... , vn
P(V): p1, p2, p3, …, pn
So, the probability distribution lists all possible variables and the outcome probabilities. The sum of all probabilities in a probability distribution must be one.
Weightage of Probability Distribution
The topic “probability distribution” is a part of the chapter “Probability” in the class 12 mathematics syllabus. This topic carries a weightage of around 7-8 marks in the examination.
Illustrated Examples on Probability Distribution
1. A discrete random variable X has the following probability distribution:
| V |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| P(V) |
K |
2K |
2K |
3K |
K2 |
2K2 |
7K2 +K |
Find the value of K. Also, calculate the mean.
Solution:
We know that,
So, K + 2K+ 2K + 3K + K2 + 2K2 + 7(7K2 +K) = 1
=> 10K2 + 9K- 1= 0 => (10K -1)(K+1) =0
=> K= 1/10 or K= -1
Since probability cannot be negative, K= 1/10.
Mean=
= 1 x (1/10) + 2x 2(1/10) + 3x 2(1/10) + 4x 3(1/10) + 5x (1/10)2 + 6x 2(1/10)2 + 7x {7(1/10)2 + 1/10}
= 1/10 + 4/10 + 6/10 + 12/10 + 5/100 + 12/100 + 49/100+ 7/10
Mean= 3.66
2.Show the probability distribution of the number of heads in three tosses of a coin.
Solution:
Let D denote the number of heads tossed. So, D can take the values 0, 1, 2, 3. When a coin is tossed three times, we get
Sample Space S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
P (D = 0) = P (no head) = P (TTT)= ⅛
P (D = 1) = P (one head) = P (HTT, THT, TTH) = ⅜
P (D = 2) = P (two heads) = P (HHT, HTH, THH) = ⅜
P (D = 3) = P (three heads) = P (HHH)= ⅛
Hence, the probability distribution of D is given as-
| D |
0 |
1 |
2 |
3 |
| P(D) |
1/8 |
3/8 |
3/8 |
1/8 |
FAQs on Probability Distribution
Q: What are the conditions of the probability distribution?
Q: What are the types of the probability distribution?
A: The probability distribution is classified as—cumulative probability distribution and discrete probability distribution.
Q: What are some examples of the normal probability distribution?
A: Roll of dice, toss of a coin, weight of population, size of clothes, students performance report, are all examples of a normal probability distribution.
Q: What is a binomial probability distribution?
A: The word binomial means this distribution works on only two outcomes. A binomial distribution is used when the outcomes are either of the two possible cases, such as positive and negative results.
Q: What is the Poisson probability distribution?
A: The Poisson probability distribution represents the probability of a given number of events happening in a fixed time or space.
News & Updates
Probability Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test

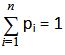
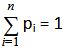 =
=