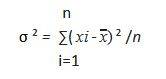Rachit Kumar SaxenaManager-Editorial
Whats is Variance and Standard Deviation?
Standard deviation and variance are concepts of statistics that are calculated with the help of the mean or average. These concepts are used in various fields, such as accounting, economics, and even in the financial sector.
Variance
The variance is the average of the squared differences from the mean.
Formula-
xi = the ‘i’ th data point
x=the mean of all data points
n=the number of data points
Standard deviation
Standard deviation is calculated from the derived variance as mentioned above. The square root of the variance generates the standard deviation.
Formula-
Weightage of Variance and Standard Deviation
The topic is introduced for the first time to the students in Grade 11 as a part of the chapter Statistics. Students can expect questions based on this concept in various competitive examinations.
Illustrative Examples on Variance and Standard Deviation
1. Find the mean and standard deviation using the short-cut method.
| xi |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
| fi |
2 |
1 |
12 |
29 |
25 |
12 |
10 |
4 |
5 |
Solution.
| xi |
fi |
di=xi -a,a=65 |
fidi |
(xi-x)² |
fi(xi-x)² |
| 60 |
2 |
-5 |
-10 |
16 |
32 |
| 61 |
1 |
-4 |
-4 |
9 |
9 |
| 62 |
12 |
-3 |
-36 |
4 |
48 |
| 63 |
29 |
-2 |
-58 |
1 |
29 |
| 64 |
25 |
-1 |
-25 |
0 |
0 |
| 65 |
12 |
0 |
0 |
1 |
12 |
| 66 |
10 |
1 |
10 |
4 |
40 |
| 67 |
4 |
2 |
8 |
9 |
36 |
| 68 |
5 |
3 |
15 |
16 |
80 |
| ∑fi =N=100 |
∑ fidi=-100 |
∑fi(xi-x)²=286 |
Mean (x)=a + ∑ fidi/ ∑fi = 65 +(-100)/100 = 65-1 = 64
Variance (σ²) = 1/N∑ fi(xi-x)² = 1/100 ×286 = 2.86
Standard deviation = √ Variance = √ 2.86 = 1.69
2. Find the mean and variance for the first ‘n’ natural numbers.
Solution.
Mean (x) = Sum of all observations/ Number of observations
Thus, (x)= [n(n+1)/2] / n = n+1/2
Variance (σ²) = 1/N∑ fi(xi-x)²
= 1/n∑ [xi(n+1/2)]²
=1/n[n(n+1)(2n+1)/6 - (n+1/n)[n(n+1)/2] +(n+1)²/4n×n
=[(n+1)(n-1)]/12
=[n² - 1]/12
3. Find the mean, variance, and standard deviation using the short-cut method
| Classes |
0-30 |
30-60 |
60-90 |
90-120 |
120-150 |
150-180 |
180-210 |
| Frequency |
2 |
3 |
5 |
10 |
3 |
5 |
2 |
Solution.
| Class |
fi |
xi |
yi=(xi-105)/30 |
(yi)² |
fiyi |
fiyi² |
| 0-30 |
2 |
15 |
-3 |
9 |
-6 |
18 |
| 30-60 |
3 |
45 |
-2 |
4 |
-6 |
12 |
| 60-90 |
5 |
75 |
-1 |
1 |
-5 |
5 |
| 90-120 |
10 |
105 |
0 |
0 |
0 |
0 |
| 120-150 |
3 |
135 |
1 |
1 |
3 |
3 |
| 150-180 |
5 |
165 |
2 |
4 |
10 |
20 |
| 180-210 |
2 |
195 |
3 |
9 |
6 |
18 |
| 30 |
2 |
76 |
Mean (x)=a + ∑ fiyi/ N× h = 105 +2/30×30 = 107
Variance (σ²) = h²/N² [N∑ fiyi²-(∑ fiyi)²]
=(30)²/(30)² [30×76 - (2)²]
=2276
FAQs on Variance and Standard Deviation
Q: How are variance and standard deviation related?
Q: What common parameters do both standard deviation and variance use?
Q: Are variance and standard deviation considered in the same unit of measurement?
Q: Why is the standard deviation always positive?
Q: Give an example of where standard deviation and variance are used?
News & Updates
Maths Statistics Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test