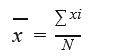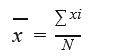Sample Statistics is defined as any figure calculated from your sample data, for example, sample average, sample standard deviation, median, and percentiles. However, whenever your statistical data like median, median, or any other statistics comes from a fraction of information and part of a population is known as Sample Statistics.
Sample Statistics Formula
Here are the formulas of sample statistics for mean, and the standard deviation is as follows:
Sample Standard Deviation Formula
The standard deviation of the small sample statistics is calculated using the formula √(∑(xi−x̄)2/n). In order to obtain an unbiased estimation of the sample standard deviation, the n is the numerator, which is replaced by n-1 so that the formula will be:
Sample Mean Formula
The calculation of the Sample Mean is a little bit different from calculating the population mean. In order to compute the Sample mean, we just have to add all the data values and divide this substitution by the number of figures present in the data set. Thus, the Sample mean is as follows:
Symbols of Sample Statistics
There are various symbols that are used of sample statistics for parameters, and statistics are as follows
| Characteristic |
Sample Statistic |
Population Parameter |
|---|---|---|
| Mean |
x̄ |
μ |
| Standard deviation |
s |
σ |
| Proportion |
p^ |
p |
- Weightage of Sample Statistics
- Illustrative Examples on Sample Statistics
- FAQs on Sample Statistics
Weightage of Sample Statistics
Sample Statistics is a topic from the chapter Statistics. The chapter has weightage around 9 to 11 marks in class X. Aspirants are facing around 3 to 4 questions of statistics in the examination every year. Statistics is also a part of class XI, XI, and XII. Apart from Sample Statistics, there are also various other significant topics covered in this chapter, such as:
- Sample Standard Deviation
- Mean
- Median
- Mode
Illustrative Examples on Sample Statistics
1. The following are the GPA scores of 30 secondary institutions. Find out the sample mean.3.1, 2.9, 2.8, 2.9, 3.8, 4.8, 4.2, 3.9, 3.4, 2.5, 4.2, 3.7, 3.3, 2.1, 3.8, 3.0, 3.7, 4.0, 2.7, 3.8, 3.2, 3.5, 3.5, 3.6, 2.2, 3.1, 3.5, 4.0, 2.7, 4.5.
Solution:
Using the given below formula to compute sample mean:
= (102.4/30)
= 3.41
Thus, the Sample mean is 3.41
2.Some students' total marks in science examinations are 101, 161, 155, 96, and 33. Find out the Sample mean marks.
Solution:
x̄ = 101+161+155+96+33/5
x̄ = 119.2
Hence, the sample marks are 119.2.
FAQs on Sample Statistics
Q: What is Statistics?
Q: What is Sample Statistics?
Q: How do you find Sample Statistics?
- Make the addition of all sample items.
- Divide sum by the number of samples you have.
- As a result, you will get mean.
- After that, use that means to find a variance.
- Now, Use the variance to find the standard deviation.
Q: What is the usage of Sample Mean?
Q: What is the formula of Sample Mean and sample standard deviation?
Maths Statistics Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test