
Salviya AntonySenior Executive - Content
Rate Constant: A rate constant, often denoted by the symbol k, is an important parameter in chemical kinetics that quantifies the rate at which a chemical reaction proceeds. In simple terms, it represents the proportionality constant between the rate of a reaction and the concentrations of the reactants raised to some power, as determined by the reaction's rate law.
This article explain the concept of rate constant, its importance, and the formula for rate constant. In NCERT Class 12 Chemistry, rate constant comes in chapter Chemical Kinetics.
Rate Constant: Important Points
- Rate constant is denoted by k.
- The rate constant is defined as the constant which defines the relationship between the molar concentration of the reactants and the rate of the chemical reaction.
- Rate constant is dependent on the temperature.
Rate Constant: Formula
The Arrhenius equation provides insight into the temperature dependence of the rate constant:
k = A. e-Ea/rt
Here, A is the pre-exponential factor or frequency factor
Ea is the activation energy
R is the gas constant
T is the absolute temperature.
This equation illustrates that the rate constant increases exponentially with temperature, emphasizing the temperature sensitivity of reaction rates.
Units of Rate Constant
| Order of reaction | Unit of rate constant |
|---|---|
| Zero order | mol L-1 s-1 |
| First order | s-1 |
| Second order | mol-1 L s-1 |
Understanding rate constants is crucial for predicting and controlling reaction rates in various chemical processes. The knowledge of rate constants aids in optimizing reaction conditions, designing efficient reaction pathways, and ensuring the practical applicability of chemical reactions in diverse fields, including industrial processes and environmental studies.
FAQs on Rate Constant
Q: The decomposition of dimethyl ether leads to the formation of CH4 , H2 and CO and the reaction rate is given by Rate = k [CH3OCH3 ] 3/2 The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e., Rate= k(PCH3OCH3)^3/2 If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?
A: Rate of given chemical reaction will be represented as
-d[pCH3OCH3] / dt
Hence units of rate is bar min-1
To find units of K, K = rate/[pCH3OCH3]3/2
The unit of k = bar -1/2min-1.
Units of Rate- bar min-1. and Units of Rate constant K : bar -1/2min -1
Q: The rate constant for a first order reaction is 60 s^–1. How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?
A: Given:
Order of the reaction = 1
Let, Initial concentration [R]°= x
Final concentration [R] = x/16
Rate constant k = 60 s-1
We know, time
t= 2.303 / k log R0 / R
t = 2.303 / 60 log (x/x/16)
t = 2.303 / 60s-1 log (1/1/16)
t = 2.303 X log 16 / 60s-1
Solving, we get t = 4.6 × 10-2s
Q: A first order reaction takes 40 min for 30% decomposition. Calculate t1/2.
A: Given:
Time t = 40 min
When 30% decomposition is undergone, 70% is the concentration.
We know, time taken
t= 2.303/K log R0 / R
Where, k- rate constant
[R]0 - initial concentration
[R] - concentration at time 't'
40 = 2.303/K log R0 / 0.7 R0
40 = 2.303/K log 1 / 0.7
40 / 0.1549 = 2.303 / k
⇒258.23 = (2.303/k)
We know, Half-life t1/2 = 0.693/k
Which can be written as, t1/2 = 0.3010 × (2.303/k)
⇒t1/2 = 0.3010 × 258.23
⇒t1/2 = 77.72 min
Q: For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained. Calculate the rate constant.
A:
|
t (sec) |
P(mm of Hg) |
|
0 |
35.0 |
|
360 |
54.0 |
|
720 |
63.0 |
A 4.20 When t = 0, the total partial pressure is P0 = 35.0 mm of Hg
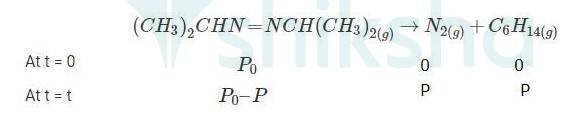
When time t = t, the total partial pressure is Pt = P0 + p
P0-p = Pt-2p, but by the above equation, we know p = Pt-P0 Hence, P0-p = Pt-2( Pt-P0)
Thus, P0-p = 2P0 – Pt
We know that time
t= 2.303/K log R0 / R
Where, k- rate constant
[R]° -Initial concentration of reactant
[R]-Concentration of reactant at time ‘t’
Here concentration can be replaced by the corresponding partial pressures.
Hence, the equation becomes,
t= 2.303/K log P0 / P0 - P
t= 2.303/K log P0 / 2P0 - Pt
→ equation 1
At time t = 360 s, Pt = 54 mm of Hg and P0 = 30 mm of Hg, Substituting in equation 1,
360 = 2.303/k log 30 / (2X30)-54
k= 2.175 X 10-3 s-1
At time t = 720 s, Pt = 63 mm of Hg and P0 = 30 mm of Hg, Substituting in equation 1,
720 = 2.303 / k log 30 / (2X30) - 63
Thus, k = 2.235 × 10-3 s–1
Taking average, k = (2.235 × 10-3 s–1 + 2.175 × 10-3 s–1)/2
∴k = 2.21 × 10-3 s–1.
Q: The rate constant for the decomposition of N2O5 at various temperatures is given below: Draw a graph between ln k and 1/T and calculate the values of A and Ea . Predict the rate constant at 30° and 50°C.
A:
|
T/°C |
0 |
20 |
40 |
60 |
80 |
|
105 × k/s-1 |
0.0787 |
1.70 |
25.7 |
178 |
2140 |
A 4.22 To convert the temperature in °C to °K we add 273 K.

The graph is given as:
The Arrhenius equation is given by k = Ae-Ea/RT
Where, k- Rate constant
A- Constant
Ea-Activation Energy
R- Gas constant
T-Temperature
Taking natural log on both sides,
ln k = ln A-(Ea/RT)...................... equation 1
By plotting a graph, ln K Vs 1/T, we get y-intercept as ln A and Slope is –Ea/R.
Slope = (y2-y1)/(x2-x1)
By substituting the values, slope = -12.301
⇒–Ea/R = -12.301
But, R = 8.314 JK-1mol-1
⇒ aE= 8.314 JK-1mol-1 × 12.301 K
⇒ aE= 102.27 kJ mol-1
Substituting the values in equation 1 for data at T = 273K
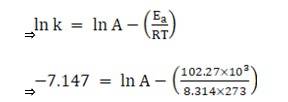
(∵ At T = 273K, ln k =-7.147)
On solving, we get ln A = 37.911
∴ A = 2.91×106
When T = 300C, hence T = 30 + 273 = 303K
⇒ ln k =-2.8
⇒ k = 6.08x10-2s-1.
When T = 500C, hence T = 50 + 273 = 323K
Substituting in equation 1,
A = 2.91 × 106, Ea = 102.27 kJ mol-1
Ln K = ln(2.91 × 106)- 102.27/(8.314 × 323)
Thus, ln k = -0.5 and k = 0.607s-1.
Q: The rate constant for the decomposition of hydrocarbons is 2.418 × 10–5s – 1 at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor?
A: Given,
k = 2.418 × 10-5 s-1 T = 546 K
Ea = 179.9 kJ mol-1 = 179.9 × 103J mol-1
The Arrhenius equation is given by k = Ae-Ea/RT Taking natural log on both sides,
Ln k = ln A-(Ea/RT) Substituting the values,
ln(2.418 × 10-5 ) = ln A-179.9/(8.314 × 546) ln A = 12.5917
A = 3.9 × 1012 s-1(approximately)
News & Updates
Atoms and Molecules Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test