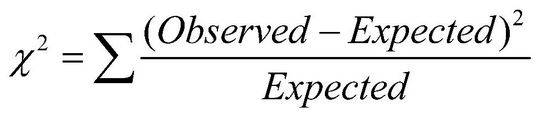Rachit Kumar SaxenaManager-Editorial
What is Chi-Square test?
The chi-square test is an essential topic in the statistics chapter of mathematics. It is a test for analyzing the data based on the observations of a set of variables. It creates a comparison between the two statistical data sets. Karl Pearson invented the test in 1900 for data analysis and distribution. Hence it was known as Pearson’s chi-squared test. The test is an estimation of the observations based on the null hypothesis.
Chi-square formula:
Χ2 denotes the Chi-Square, and the formula is:
χ2 = ∑(Oi – Ei)2/Ei
Where,
O: Observed frequency
E: expected frequency
∑: summation
χ 2: Chi-Square Value
Chi-Square Distribution
The chi-square distribution is the term for the sampling distribution of the test statistics. The test determines a vast difference between normal frequencies and observed frequencies in one or more classes. It defines the probability of independent data. The chi-square test is used for only the categorized data, like men and women under the heads of Gender, Age, Height, etc.
P-Value
The chi-square test in statistics is used for determining the P-value. P stands for probability, and its various values indicate different hypotheses.
- P≤ 0.05; When the hypothesis is rejected
- P>.05; When the hypothesis is Accepted
Both probability and statistics are related to the chi-squared test.
Types of chi-square test:
1) The independent test
2) The goodness of fit test
Weightage of Chi-Square
The chi-square test is a part of the statistics chapter in the NCERT syllabus for the 10th and 11th. The marks weightage is as follows-
10th class - 8 marks
11th class – 10 marks
Illustrative Examples on Chi-Square
1. Society of 1000 residents has four neighbourhoods, P, Q, R, and S. A sample is taken of 650 residents of the community, having doctors, engineers, and teachers. The null hypothesis states that each one’s neighbourhood is independent of their professional division. The categories are:
| Categories |
P |
Q |
R |
S |
Total |
|---|---|---|---|---|---|
| Doctors |
90 |
60 |
104 |
95 |
349 |
| Engineers |
30 |
50 |
51 |
20 |
151 |
| Teachers |
30 |
40 |
45 |
35 |
150 |
| Total |
150 |
150 |
200 |
150 |
650 |
Solution.
The sample living in neighbourhood P, 150, estimates the 1,000 people living in neighbourhood P. Hence, we take 349/650 to determine the 1,000 as doctors ratio. With the assumption of independence in the hypothesis, The expected number of doctors in neighbourhood P is-
150 x 349/650 ≈ 80.54
Using the chi-square test formula,
=(Observed – Expected)2/Expected = (90-80.54)2/80.54 ≈ 1.11
2.Find the chi-square value using the following data:
| Male |
Female |
|
|---|---|---|
| Full Stop |
6(observed) 6.24 (expected) |
6 (observed) 5.76 (expected) |
| Rolling Stop |
16 (observed) 16.12 (expected) |
15 (observed) 14.88 (expected) |
| No Stop |
4 (observed) 3.64 (expected) |
3 (observed) 3.36 (expected) |
Solution.
Chi-Square formula:
χ2 = ∑ (O − E)2 / E
Do the calculation with this formula for every cell. For example, cell 1 will have (Male/Full Stop):
Its Observed number is 6
Its Expected number is 6.24
Hence, (6 – 6.24)2 /6.24 = 0.0092
Use the same method for all the cells, and add the final values for each cell to get the Chi-Square number final value.
FAQs on Chi-Square
Q: What is a chi-square test?
Q: In which class is the topic of the chi-square test taught?
Q: What is the difference between the t-test and the chi-square test?
Q: What is the marks weightage of the topic?
Q: What is the formula of the chi-square test?
News & Updates
Statistics Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test